forms of escape
Summary
The OER I have created is based on the learning theory of the double-loop and the conceptual framework of contemporary art to question the intersubjective, prototypical category of escape. The instruction will guide the learner through a hands-on experimentation with material, form, deconstruction, and reconstruction, that echoes the double-loop of learning. At each stage, the learner is given a simple direction, backed up by a dataset of ideas, materials, actions, or questions.
double-loop © 2025 by Kirsty Smith is licensed under CC.
Introduction
This toolkit is for those stuck in a loop.
The instructions provided may be used to escape from a physical, mental, or imaginary situation. The learner will engage in double-loop thinking by following instructions to write a short text; this process can be applied to a project, artwork, problem, or thought experiment.
Single-loop learning occurs as errors are corrected by improvising existing systems and revising failures. In the second, the learner is asked to reflect upon the internal thinking processes and values. The diagram below shows a model of this thinking:
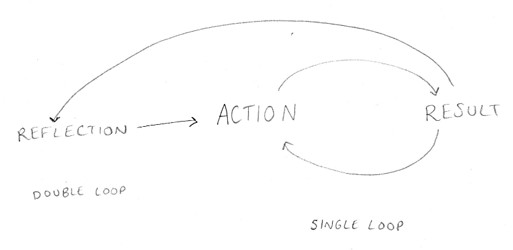
double-loop process © 2025 by Kirsty Smith is licensed under CC.
To escape the first loop, the learner must discover alternatives to redrafting old values into new action by questioning their own integral principles and beliefs.
The toolkit offers a list of suggestions in every step to engage you in creative decision-making and critical thinking.
AIMS
The learning aims of this OER is to discover feedback loops within their own thinking, open to self-reflection on failure. The toolkit encourages self-expression through writing a short text, helping learners develop self-awareness and prepare for future possibilities.
Engage in double-loop thinking to develop a form of escape by following these steps:
Think of a time where you have repeated failure. This may be a rejection, a habit, an exam, a bad mark, an emotional reflection, falling into a situation or a social or interpersonal experience.
(4 mins)
Express how you can escape this spiral of failure. Think of the form of escape, imagine any design. Form your thought into reality by writing a short statement.
There is no right or wrong way to escape, nor is there any right or wrong thing, feeling, or situation to escape from.
Do not relay personal failure instead reframe it, own it, utilize it into a new process
(4 mins)
Distance it from the thought, redact and remove the original idea from your work.
This can be done by crossing-out with black ink, or online tools like adobe PDF or www.ilovepdf/redact-pdf
(2 mins)
Example:

Swap, share with someone. Do not try and guess what the escape is, only engage in the process. Ask yourself if you can use this process, if not you may want to edit, suggest or comment.
If you are doing this by yourself you can imagine yourself as separate from the work.
(2 mins)
Example:

example of edited text © 2025 by Kirsty Smith is licensed
Swap back
Return to your own idea.
Reflect thoughtfully on these actions, and inquire within yourself (Advocate your principles, values, and beliefs in a way that invites inquiry into them and encourages other people to do the same)
(3 mins)
Think about your original idea.
Discuss to reflect on the actions.
Do you engage in a thought process to escape a singular loop thinking?
Did you have a similar notion of a form of escape?
What assumptions did you make?
How do you feel about your previous escapism?
(3 mins)
Congratulations, you have engaged in double-loop thinking! For further reading, please visit the list below:
Argyris, Chris. “Double-Loop Learning, Teaching, and Research.” Academy of Management Learning & Education 1, no. 2 (2002): 206–18. https://doi.org/10.5465/amle.2002.8509400
Clark, Kevin. “Double-Loop Learning and Productive Reasoning: Chris Argyris’s Contributions to a Framework for Lifelong Learning and Inquiry.” Midwest Social Sciences Journal 24, no. 1 (2021): 33–52. https://doi.org/10.22543/0796.241.1042.
Einstein, Brad. 2025. “The Ladder of Inference: How to Use It & Examples.” Business Insights Blog. May 6, 2025. https://online.hbs.edu/blog/post/ladder-of-inference.
Farley, Paul. “In the Loop – 3. A Strange Loop – BBC Sounds.” 2023. BBC. 2023. https://www.bbc.co.uk/sounds/play/m001nvp8.
Joel Bird | JiveLearning. 2021. “Use Double-Loop Learning to Be More Efficient and Productive | What Is Double Loop Learning?” YouTube. April 26, 2021. https://www.youtube.com/watch?v=SnPuFjhHTno.
Schneiderheinze, Dirk . 2021. “Bach’s Crab Cannon as It Could (Actually) Sound on a Clear Möbius Strip.” YouTube. December 30, 2021. https://www.youtube.com/watch?v=oYOEKS3Xhrs.


