Stair climbing in granular sorting of an infinite chute flow with irregular particles

I recently re-discovered some simulations I did during my PhD and am as intrigued by them now as I was then – so I thought I would share them with you.

For my PhD I wrote a Discrete Element Model to simulate the evolution of mountain building. This treats the subsurface as a course granular material in a similar way to the sandbox experiments Cadell performed here in Edinburgh in the 1800’s.

The simulations I want to share are for an inclined chute flow with periodic boundary conditions. The particles are mostly clusters of 3 particles apart from one large particle which is 12 particles bonded together. This gives the particles angularity and changes how easy it is for particles to move past each other and to rotate, as compared to round particles. If you think of the emergent bulk friction of a material being its resistance to particles moving past each other, angularity will clearly increase the observed friction in the material. This was a model I wrote 16 years ago and is in 2D and took a week or so to run – clearly this could be done much faster now!

Ignore the text at the top on the animations below as this was inherited from some other analyses and it is far too long ago for me to go back and edit the code now… This is clearly not an accretionary wedge…

The first animation colours the particles in layers by their initial depths. The orange particles on the bottom are fixed and irregularly placed to provide a rough base. The single large particle is also coloured in orange and you can see it steadily rising up through the flow until it reaches the surface.

The animation below examines some of the properties of the particles in this flow.The top row shows the horizontal, vertical and absolute velocities for each particle as a function of depth on the vertical. The horizontal velocities are always positive and increase towards the upper surface; the standard deviation in these velocities is show in red dots binned buy depth; and the density of the flow with depth is shown in a black line. The vertical velocities are both positive and negative as particles can move up and down conserving the mass balance. These figures show that the flow can be broken down into a slow basal layer, a steady flow for most depths and a fluctuating high velocity layer on the top. The lower animation shows the trajectories of a subset of particles within the flow.

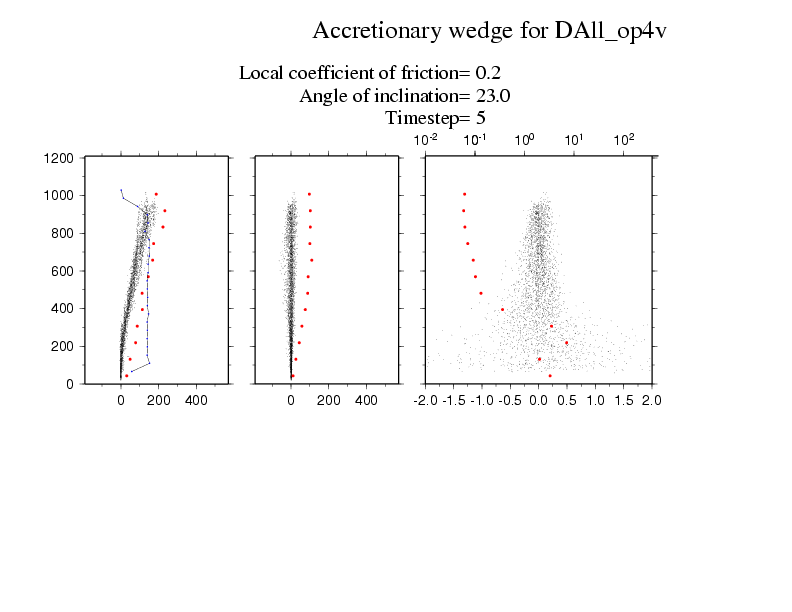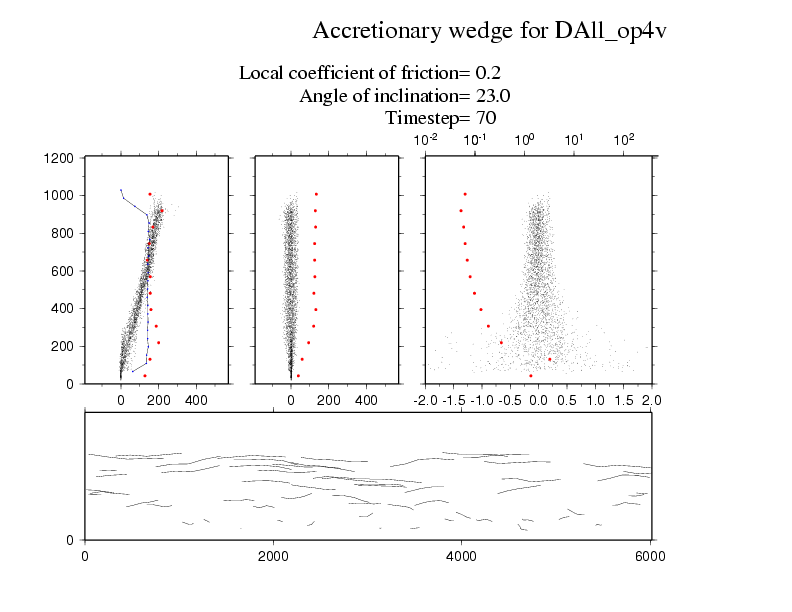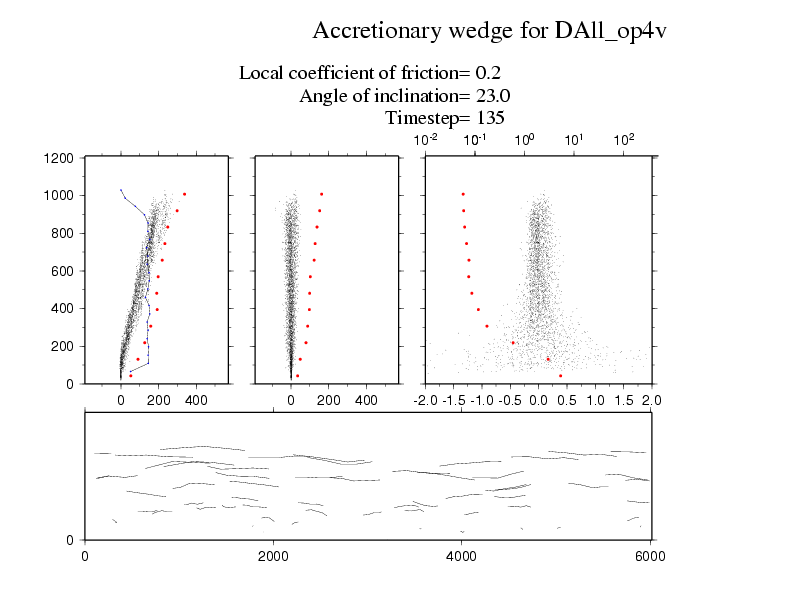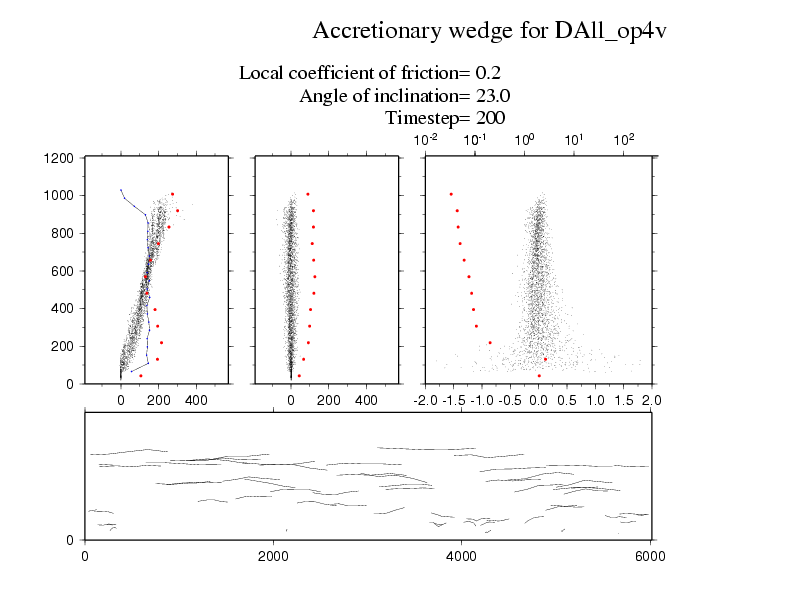
I think the most interesting presentation of this flow is the final figure. We now show all the small particles as just trajectories and the large angular particle is in green. This particle is carried by the flow for periods and then rises up to the surface in intermittent steps. What really interests me is how the rotation of this angular particle allows it to climb up through the flow as though it is climbing a staircase. I assume that this effect results because the velocity gradient can induce rotation of the angular particle which has to be accommodated by it climbing if it is moving at the same or higher speed than the particles in front of it. If it were a round particle, it would just spin with no climbing required.

Whilst size and or density difference is sufficient to induce sorting of particles in granular flows, this is an example of another mechanism by which particles can be sorted. The effect is probably stronger in this 2D simulation than it it were a 3D model – but I suspect the principle would still hold. I like this example because it combines elements of symmetry breaking, random fluctuations and emergent behaviour which are ever present is granular phenomenon.