Category: STACK

Extracting student response data from STACK

George Kinnear/ / STACK, Teaching, Technical

When students answer STACK questions, the Moodle quiz system stores lots of information about their work. How can we get access to the data to learn from it?

There is some advice about this in the STACK documentation, but here I thought I’d share my own experience of using the features.

STACK response analysis

The STACK plugin provides an overview of how students responded to the question. In particular, this shows

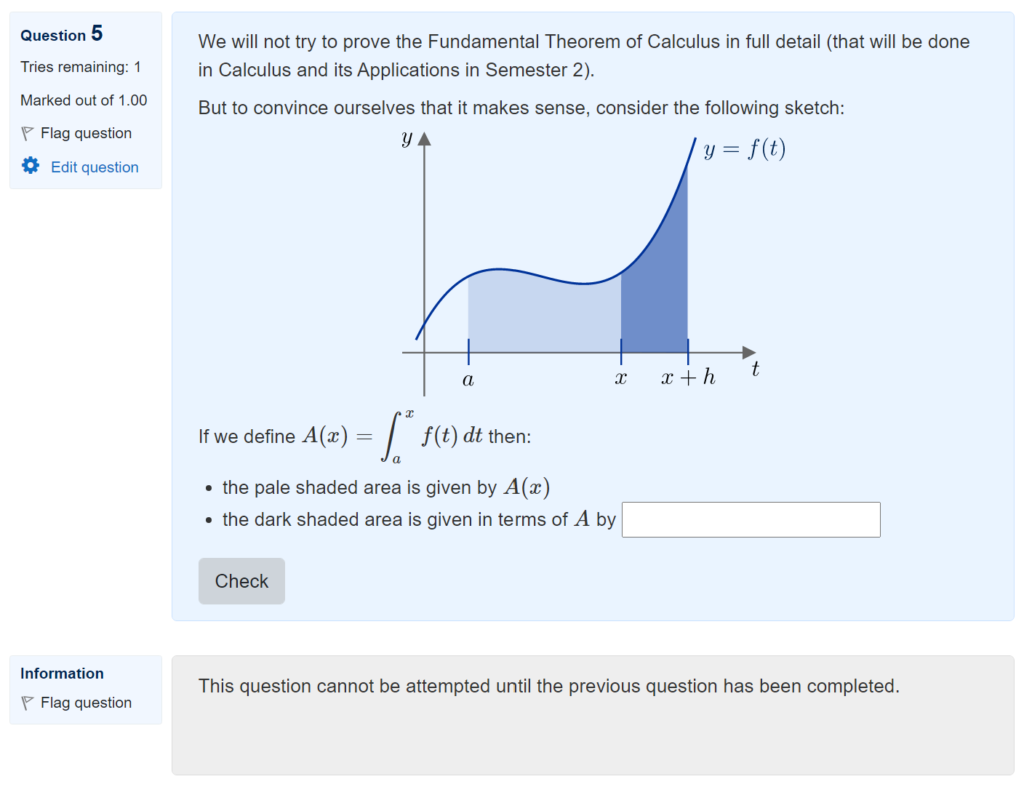
To get access to this report, as a teacher, click on the “STACK question dashboard” link at the top-right of the question:

STACK question preview, with the "STACK question dashboard" link at the top right

Then select the “Analyze responses” option from the top menu bar:

Analyze responses

I find the first section of the response analysis page quite helpful to get an overview of how frequently students ended up at different parts of the potential response tree:

Example of a STACK PRT analysis

For instance, this shows that in prt2, 78 responses (which was 15% of the total) ended up at prt2-2-T, which was a node that I included to check for a specific error and to give feedback accordingly.

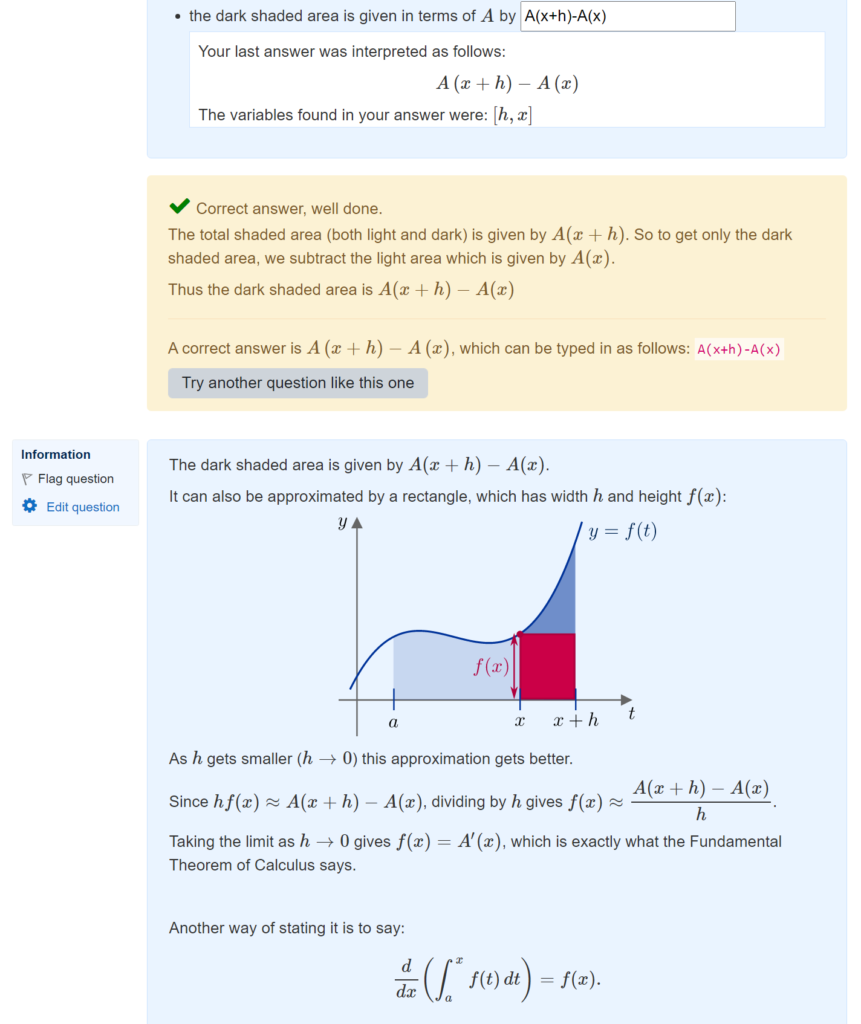
You can also see the raw data at the end of the page:

First part of the raw data

This packs in quite a lot of information! This example shows that variant number 2 was answered 75 times, and then we see the different responses ordered from most to least common – in particular, 31 of the responses were the correct answer (3/2 for ans1 and 4 for ans2 for this variant of the question).

I find it useful to use the browser’s “find text in page” search function, to look for instances of a particular PRT node that I’m interested in. If you want to do a more methodical analysis, you might want to copy/paste this data into a text file and do some processing offline.

It’s also worth checking in case there are particularly common incorrect responses that you hadn’t anticipated. Of course, it can be tricky to figure out from the final answers alone what error the students might have made! But if you can, then you may want to add a node to your PRT that gives feedback on this error. This paper gives a nice example of the process of updating a PRT based on the response data:

Alarfaj, M., & Sangwin, C. (2022). Updating STACK Potential Response Trees Based on Separated Concerns. International Journal of Emerging Technologies in Learning (iJET), 17(23), Article 23. https://doi.org/10.3991/ijet.v17i23.35929

Quiz results report

If the question attempts took place in a quiz, you can also see data about them from the quiz results report.

To see this, go to the quiz, then choose the Results tab. You’ll see a table with a row for each student, and a column for each question on the quiz. In the default “Grades” report, the entries in the table are the grades. You can also switch to the “Results” report (using the dropdown list just below the “Quiz / Settings / Questions / Results” tabs), and the entries in the table will show you the same sort of text as in the “raw data” shown above.

Here’s an example of what it looks like, where “Response 3” shows the same question as above:

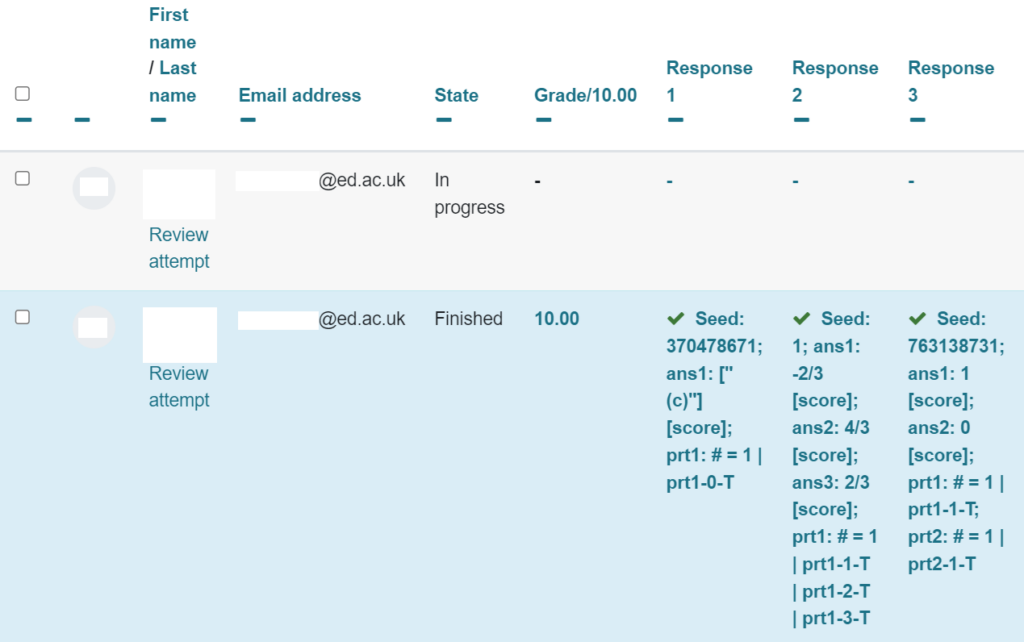
Moodle quiz results page

You can download a spreadsheet of all this data for offline work. However, it’s important to note that this table only shows the student’s last attempt at the question.

You can also click on an individual entry, to see a preview of the question.

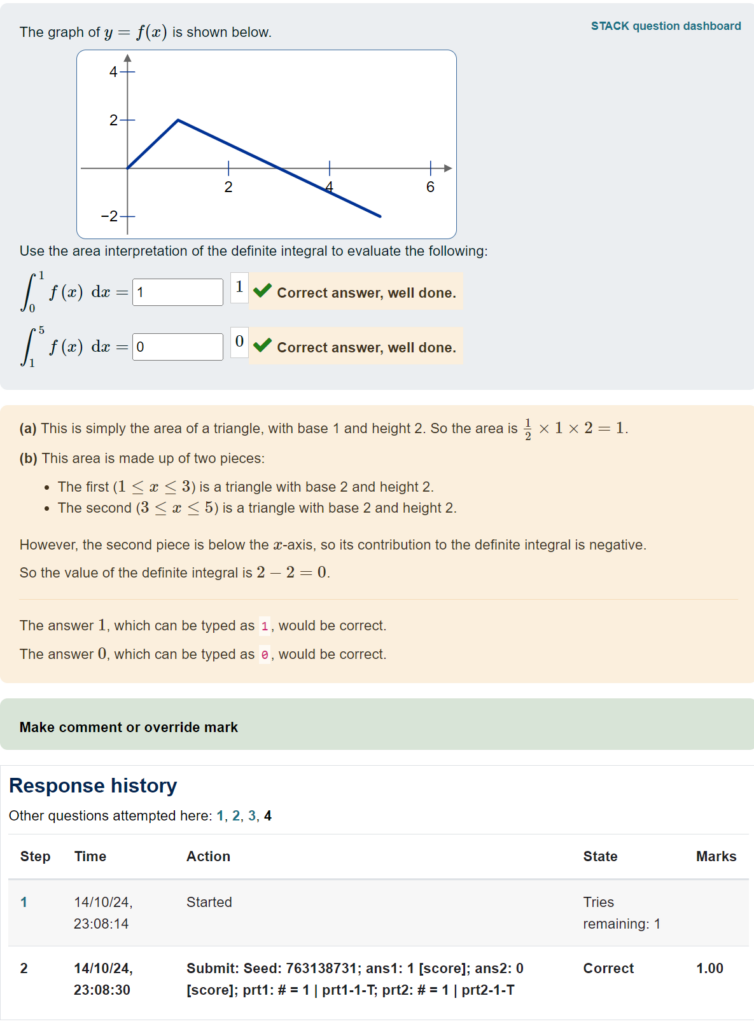
Student attempt at a STACK question

You can see at the bottom of the preview the same response summary, along with the time when the student submitted the answer.

Importantly, this quiz used “interactive mode”, so students were able to “try another question like this”. You can see at the bottom there are links “1, 2, 3, 4” to the different attempts. Here is what the student’s first attempt looked like:

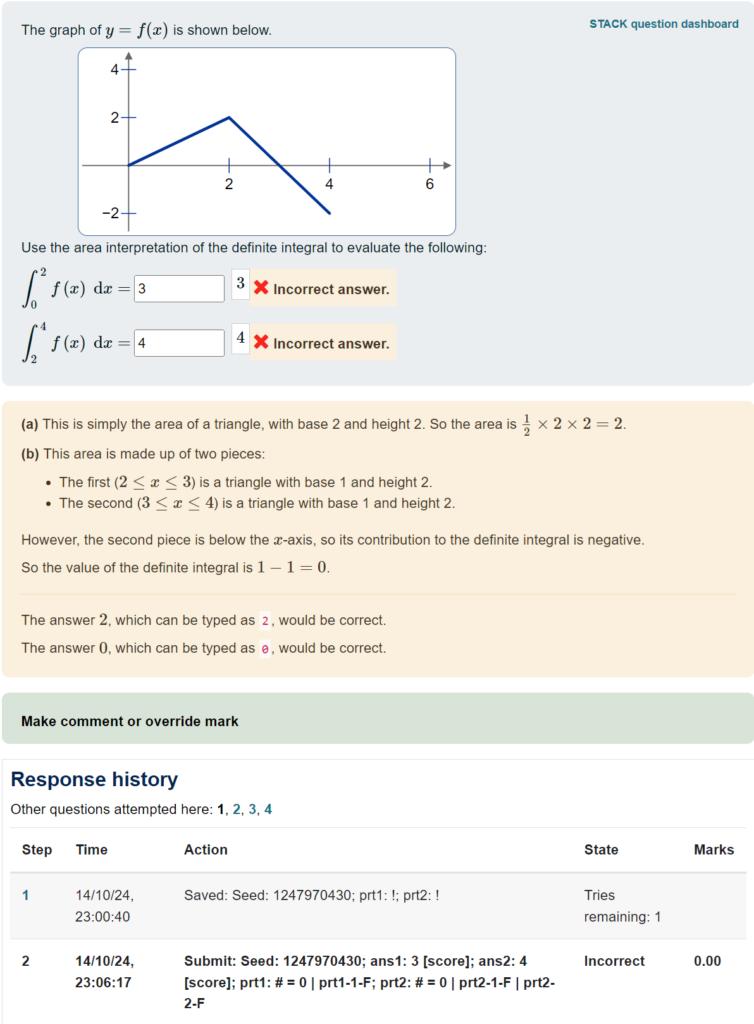
Another attempt at the same question

This lets you drill down to see how individual students worked through the questions. But it’s a very manual process…

Database query

It’s helpful to be able to be able to get access to all of the response data at once – particularly for research purposes. I first did this in a study involving hundreds of students, so it was important to be able to get all the data in an efficient way!

Since I had Moodle Administrator access, I was able to use the “Ad-hoc database queries” plugin. (If you want to use the plugin, you’ll either need Administrator access, or ask your administrator to install it and give you access to it.)

I put together an SQL query to extract all student attempts at questions in a given quiz:

SQL query (on GitHub)

When you run the query using the ad-hoc database queries plugin, you are prompted to enter the quiz id. The plugin then produces a report that you can download as a spreadsheet. Here is an excerpt of a few of the relevant columns, showing all four attempts by the student from the example above:

questionid variant questionsummary responsesummary state fraction stepdate
1617 1 [2,3,4] and [2,-2] gives 2 and 0 Seed: 1247970430; ans1: 3 [score]; ans2: 4 [score]; prt1: # = 0 | prt1-1-F; prt2: # = 0 | prt2-1-F | prt2-2-F gradedwrong 0 14/10/2024 23:06
1617 2 [1,4,5] and [3,-1] gives 3/2 and 4 Seed: 486334144; ans1: 3/2 [score]; ans2: 11/2 [score]; prt1: # = 1 | prt1-1-T; prt2: # = 0 | prt2-1-F | prt2-2-F gradedpartial 0.5 14/10/2024 23:06
1617 6 [1,2,3] and [2,-2] gives 1 and 0 Seed: 476689955; ans1: 1 [score]; ans2: -2 [score]; prt1: # = 1 | prt1-1-T; prt2: # = 0 | prt2-1-F | prt2-2-F gradedpartial 0.5 14/10/2024 23:07
1617 4 [1,3,5] and [2,-2] gives 1 and 0 Seed: 763138731; ans1: 1 [score]; ans2: 0 [score]; prt1: # = 1 | prt1-1-T; prt2: # = 1 | prt2-1-T gradedright 1 14/10/2024 23:08

Scaffolded proofs in a Moodle quiz

George Kinnear/ / FAC, STACK, Teaching

In my online course Fundamentals of Algebra and Calculus, there were several places where I wanted to encourage students to engage with a key proof while reading the text.

One approach to this is to ask proof comprehension questions after giving the proof, but I’ve also tried writing some sequences of questions that lead the students through the proof in a scaffolded/structured way.

Here’s a simple example, of a sketch proof of the Fundamental Theorem of Calculus:Screenshot of question showing a sketch and asking students to complete an expression for a shaded area in the sketch

Students can’t see the next part of the proof until they give an answer. Once they have submitted their answer, the next part is revealed:Solution to the task, followed by the rest of the proof

I’ve used this approach in other places in the course, sometimes with more than one step.

The way to do this in Moodle is by having the quiz settings set to “Interactive with multiple tries”:Then using the little padlock symbols that appear at the right-hand side between questions on the “Edit questions” page:

After clicking the padlock, it changes to locked to indicate that students must answer the first question to see the second:

I’ve not done any serious evaluation of this approach, but my intuition is that it’s a good way to direct students’ attention to certain parts of a proof and encourage them to be more active in their reading.

STACK: Checking answers in polar form

George Kinnear/ / FAC, STACK, Teaching

Last week’s topic in FAC was complex numbers, and I’ve had some difficulties with STACK questions asking students to give their answer in polar form, e.g. when the correct answer was 4*(cos(pi/3)+i*sin(pi/3)) an answer of 4*(cos((1/3)*pi)+i*sin((1/3)*pi)) would be marked incorrect!

The issue was that:

  • with simplificatiwon turned on, Maxima will automatically simplify polar form to cartesian form, so I need simplification off.
  • with simplification off, Maxima won’t see those equally valid ways of writing the argument as the same.

I was using the EqualComAss answer test to check whether the student answer (ans1) was equal to the model answer (ta1), and this was failing in the cases above.

The solution I came up with is to add some code to the feedback variables box at the top of the PRT, to replace cos and sin with alternate versions so that Maxima can’t simplify the expressions to cartesian form. I can then use ev(…,simp) to make use of simplification when comparing the expressions:

form_ans1:subst([cos=COSINE, sin=SINE], ans1);
form_ta1:subst([cos=COSINE, sin=SINE], ta1);
proper_form:is(ev(expand(form_ans1-form_ta1),simp)=0);

This will ensure that COSINE(pi/3) and COSINE((1/3)*pi) will cancel out, thanks to the simplification being turned on.

But since Maxima doesn’t know anything about COSINE, it can’t cancel out COSINE(-pi/3) and COSINE(5pi/3) (as it would do with cos) if students give their answer with the wrong value for the principal argument.

It was then just a case of replacing the test for EqualComAss(ans1,ta1) in the PRT with a test that AlgEquiv(proper_form, true), and regrading. Out of ~160 attempts this picked up 8 students who deserved full marks!

Update (08/11/2021): One year on, and STACK now has a new feature which makes it easier to grade these answers correctly! The new EqualComAssRules answer test lets you add a list of different algebraic rules so that two answers should count as equivalent if they differ only by those rules – e.g. x and 1*x.

To fix this question, it’s enough to change the first PRT node to the following, using the “Test options” box to specify the list of algebraic rules:

ATEqualComAssRules(ans1, ta1, [ID_TRANS,NEG_TRANS,DIV_TRANS,INT_ARITH]);