Category: FAC

You can see more about this course here: https://blogs.ed.ac.uk/georgekinnear/fundamentals-of-algebra-and-calculus/

Moodle quiz settings

George Kinnear/ / FAC, Teaching

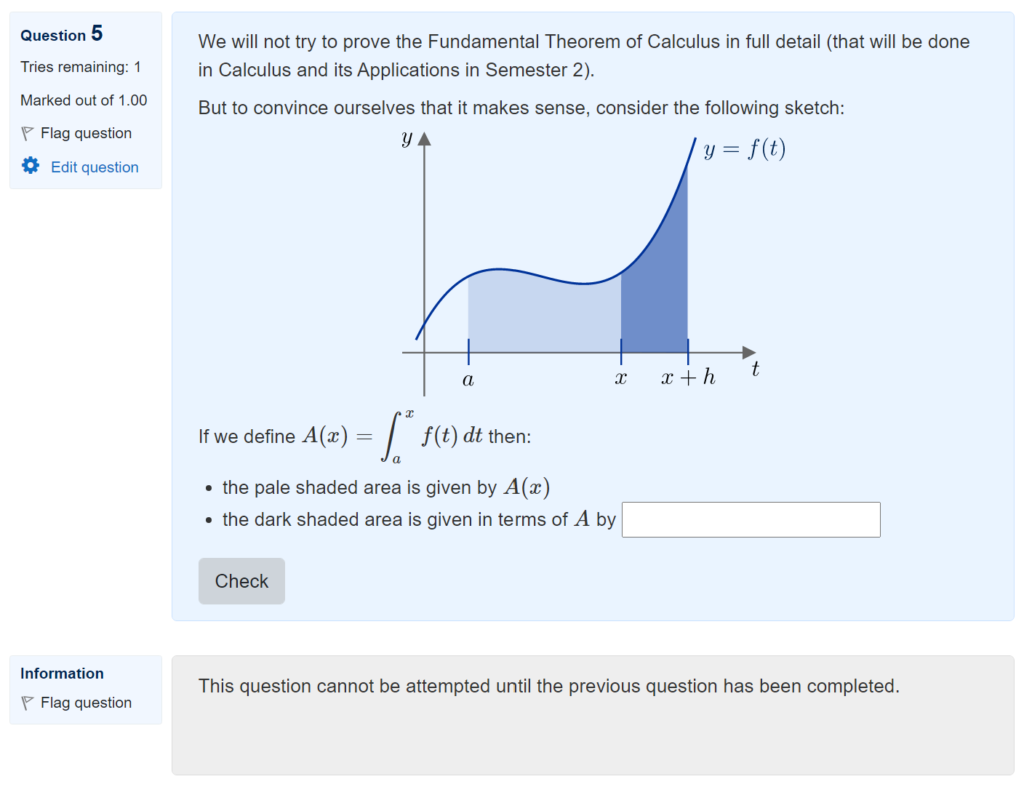
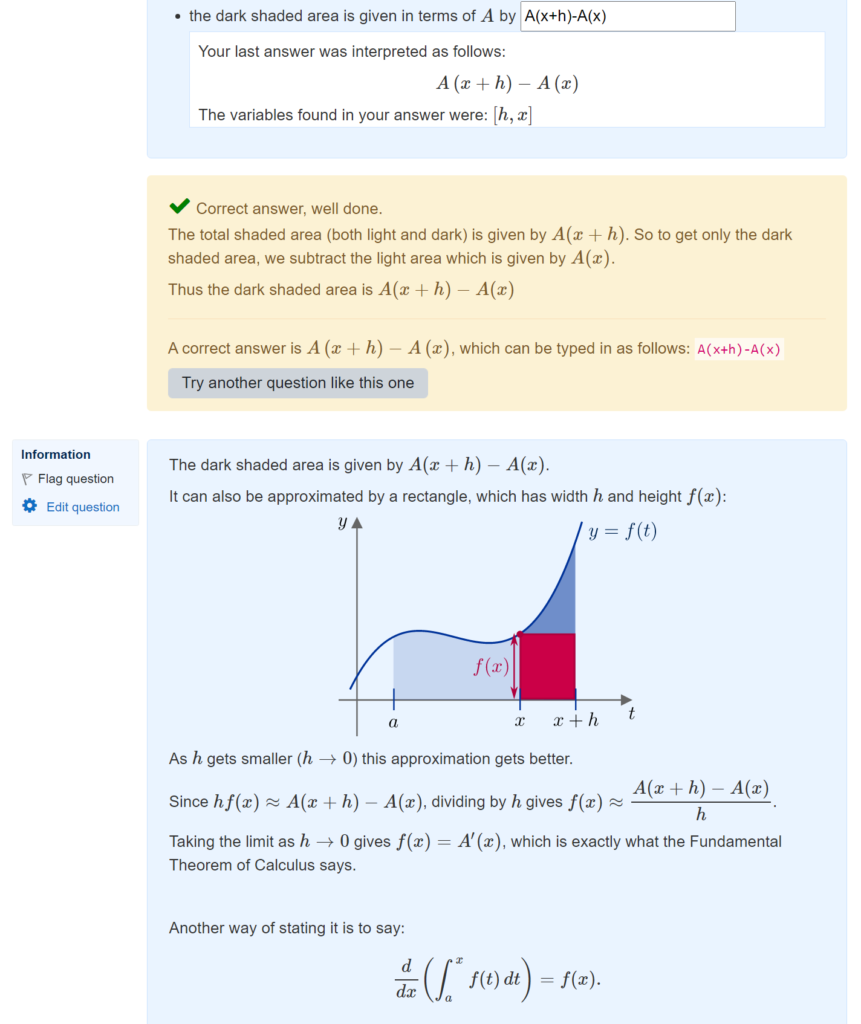
The Moodle quiz offers a huge range of settings for the timing, number of attempts, and feedback that is offered to students. Deciding how best to use these options is a tricky question – and actually forms the basis for some of the questions in the research agenda that I recently developed in collaboration with several colleagues:

Roles of e-assessment in course design

Q27. How can formative e-assessments improve students’ performance in later assessments?
Q28. How can regular summative e-assessments support learning?
Q29. What are suitable roles for e-assessment in formative and summative assessment?
Q30. To what extent does the timing and frequency of e-assessments during a course affect student learning?
Q31. What are the relations between the mode of course instruction and students’ performance and activity in e-assessment?

I’m sure that I’ve not explored the full potential of all the Moodle quiz options, but here are some examples of settings that I use in my Fundamentals of Algebra and Calculus course.

Course materials

For the course materials within FAC, I have put all the feedback settings to the max, including the option to redo individual questions:

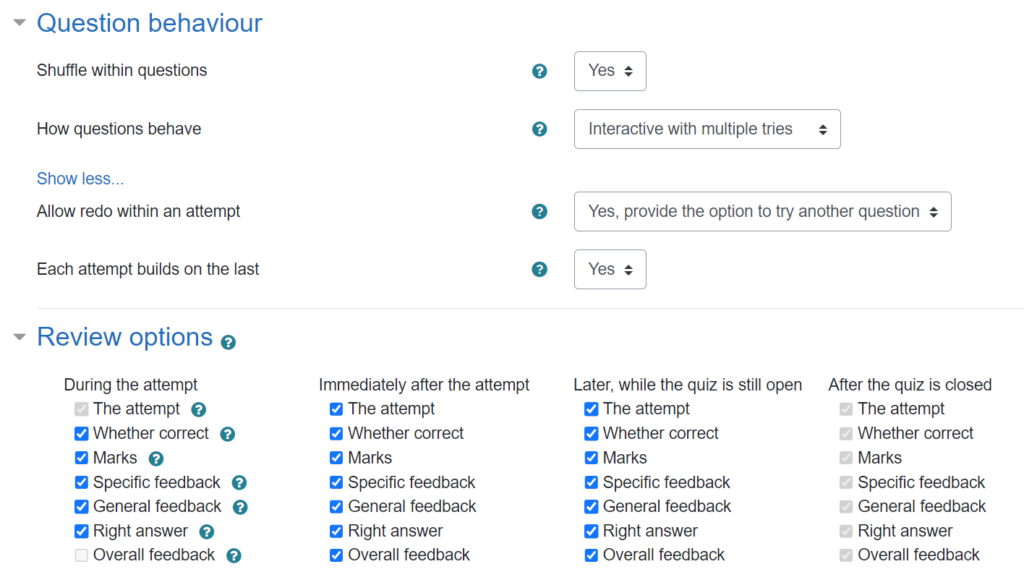
Moodle quiz settings, including "interactive with multiple tries"

The “scores” on those quizzes really don’t matter for anything, and actually most students never even submit the whole quiz to be graded, since they can see the results question-by-question as they go through.

Practice quizzes

Each week there is an assessed quiz that contributes to the students’ grades (see below) – but before they can take that quiz, they need to score at least 80% on the week’s Practice Quiz.

For the Practice Quiz, students can have an unlimited number of attempts – but there is no way to replace individual questions. Instead, students need to complete the whole quiz and submit it to get their score at the end (as preparation for the way it will work in the assessed quiz).

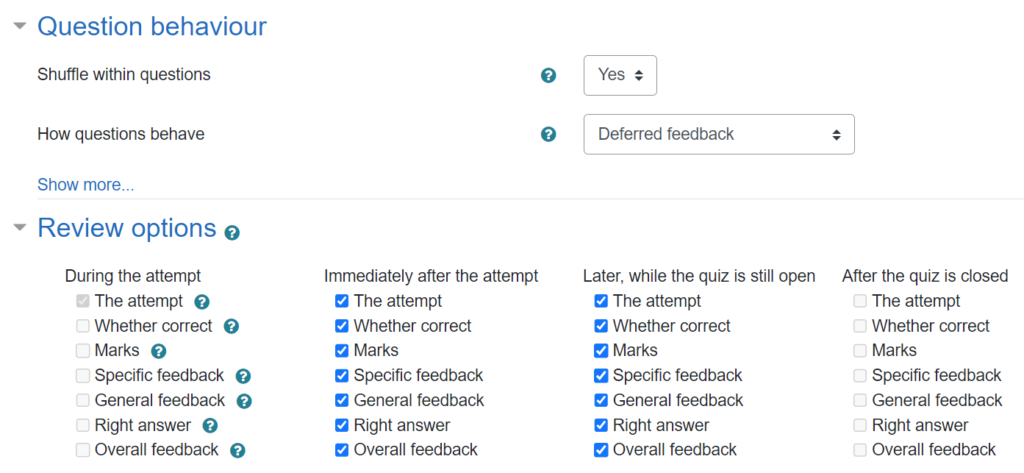
Moodle quiz settings - deferred feedback

Assessed quizzes

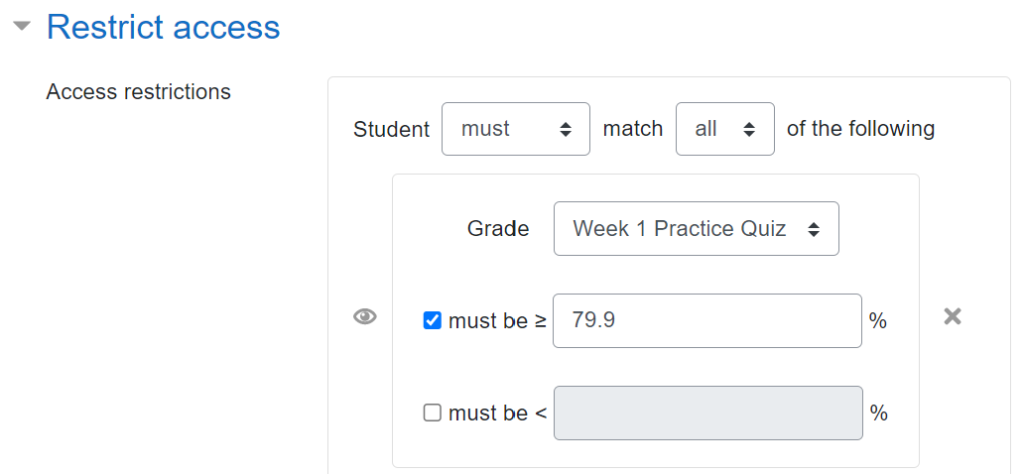
Each week there is a “Final Test” quiz that contributes to the students’ grades. Scores of over 80% are a “Mastery” result, and students need to get at least 7 Mastery results across the 10 weeks to pass the course. The grading scheme is a bit more complicated than that; you can see the full details in my paper about the course design and my post about how to set it up in the Moodle gradebook.

Having the requirement to score at least 80% on the Practice Quiz (which typically has very similar tasks to the Final Test) means that students should be well-prepared to succeed.

Moodle restrict access settings

The Final Test itself uses more restrictive settings to control when feedback is available, since I wanted to avoid having worked solutions circulating while other students have yet to complete the quiz. In particular, the “general feedback” (i.e., worked solution) and “right answer” are only available after the quiz is closed:

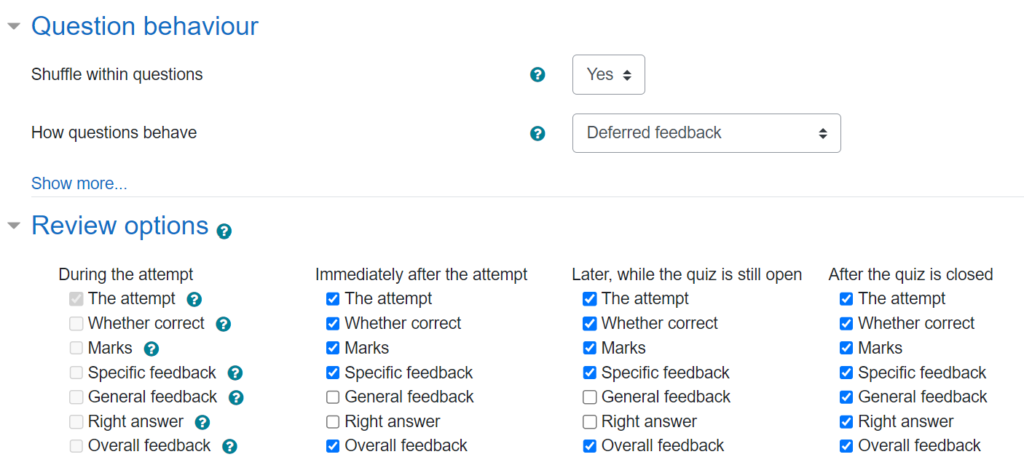
Moodle quiz settings with deferred feedback available after deadline

There is only 1 attempt allowed at this quiz, with a time limit of 90 minutes from when the quiz is opened. Students need to complete each week’s quiz by a regular deadline. However, if students don’t meet the Mastery threshold, there is a resit version that becomes available the next day (again, set up using the “restrict access” feature so that it only appears for students who need it).

Other approaches?

As I mentioned, I’ve only scratched the surface of what’s possible with the Moodle quiz settings. I know other colleagues have set up quizzes where students can make multiple attempts, and the grade is based on the average of the attempts (so as to incentivise trying hard on the first attempt, but allowing for students to improve if they’re not happy with a bad first attempt). It’s also possible to set penalties within questions, so that you can use the interactive quiz mode (like the course materials example above): that allows students to redo an individual question if they’re not happy with the score, but possibly with a penalty (again, to encourage students to take the first attempt seriously).

Scaffolded proofs in a Moodle quiz

George Kinnear/ / FAC, STACK, Teaching

In my online course Fundamentals of Algebra and Calculus, there were several places where I wanted to encourage students to engage with a key proof while reading the text.

One approach to this is to ask proof comprehension questions after giving the proof, but I’ve also tried writing some sequences of questions that lead the students through the proof in a scaffolded/structured way.

Here’s a simple example, of a sketch proof of the Fundamental Theorem of Calculus:Screenshot of question showing a sketch and asking students to complete an expression for a shaded area in the sketch

Students can’t see the next part of the proof until they give an answer. Once they have submitted their answer, the next part is revealed:Solution to the task, followed by the rest of the proof

I’ve used this approach in other places in the course, sometimes with more than one step.

The way to do this in Moodle is by having the quiz settings set to “Interactive with multiple tries”:Then using the little padlock symbols that appear at the right-hand side between questions on the “Edit questions” page:

After clicking the padlock, it changes to locked to indicate that students must answer the first question to see the second:

I’ve not done any serious evaluation of this approach, but my intuition is that it’s a good way to direct students’ attention to certain parts of a proof and encourage them to be more active in their reading.

Moodle gradebook setup for mastery grading

George Kinnear/ / FAC, Teaching

In my course Fundamentals of Algebra and Calculus, students complete weekly Unit Tests. Their grade is determined by the number of Unit Tests passed at Mastery (80%+) or Distinction (95%+) levels. For instance, to pass the course, students need to get Mastery in at least 7 of the 10 units. You can find more details about the course in this paper:

  • Kinnear, G., Wood, A. K., Gratwick, R. (2021). Designing and evaluating an online course to support transition to university mathematics. International Journal of Mathematical Education in Science and Technology. https://doi.org/10.1080/0020739X.2021.1962554

All the Unit Tests are set up as Moodle quizzes, and I needed a way to compute the number of tests completed as Mastery level (and at Distinction level) for each student.

To make matters more complicated, there are 4 different versions of each Unit Test:

  • Unit Test – the first attempt
  • Unit Test Resit – a second attempt, available to students shortly after the first attempt if they did not reach Mastery
  • Unit Test (Extra Resit) – a third attempt, available at the end of semester
  • Unit Test (Resit Diet) – a fourth attempt, available during the resit diet in August

Each subsequent attempt replaces the result of previous ones – e.g. if a student with a Mastery result on the first attempt decides to take the Unit Test (Extra Resit) to try to get a Distinction, then they will lose the Mastery result if they do not reach the 80% threshold.

To set this up in the Moodle gradebook, I have given each of the variants an ID, with the pattern:

  • WnFT
  • WnFTR
  • WnFTR2
  • WnFTRD

(where n is the week number).

Then I have added a calculated grade item called “Number of Mastery results”, with a complicated formula to determine this. It is the sum of 10 terms like this:

ceil([[W1FTRD]]/32)*floor([[W1FTRD]]/25.5)+(1-ceil([[W1FTRD]]/32))*(ceil([[W1FTR2]]/32)*floor([[W1FTR2]]/25.5)+(1-ceil([[W1FTR2]]/32))*floor(max([[W1FT]],[[W1FTR]])/25.5))

where this snippet computes the number of Mastery results in week 1 (i.e. it will return 0 or 1).

Note that the 25.5 appears throughout this expression because that is the threshold for 80% on these tests.

  • ceil([[W1FTRD]]/32)*floor([[W1FTRD]]/25.5) means “if they took the Resit Diet version, then use their score on that to decide if they got a Mastery result”
  • (1-ceil([[W1FTRD]]/32))*(...) means “if they didn’t take the Resit Diet version, then use their other scores to decide”
  • There’s then a similar pattern with W1FTR2
  • And finally, if students didn’t take either W1FTRD or W1FTR2, we use the best of the W1FT and W1FTR results to decide (simple “best of” is OK here, since students can only take W1FTR if they did not get Mastery on W1FT).

This is all quite complicated, I know! It has grown up over time, as the FTR2 and FTRD versions were added after I first set up this approach.

Also, when I first implemented this, our version of Moodle did not support “if” statements – since the Moodle grade calculations can now make use of “if” statements, this calculation could be greatly simplified.

STACK: Checking answers in polar form

George Kinnear/ / FAC, STACK, Teaching

Last week’s topic in FAC was complex numbers, and I’ve had some difficulties with STACK questions asking students to give their answer in polar form, e.g. when the correct answer was 4*(cos(pi/3)+i*sin(pi/3)) an answer of 4*(cos((1/3)*pi)+i*sin((1/3)*pi)) would be marked incorrect!

The issue was that:

  • with simplification turned on, Maxima will automatically simplify polar form to cartesian form, so I need simplification off.
  • with simplification off, Maxima won’t see those equally valid ways of writing the argument as the same.

I was using the EqualComAss answer test to check whether the student answer (ans1) was equal to the model answer (ta1), and this was failing in the cases above.

The solution I came up with is to add some code to the feedback variables box at the top of the PRT, to replace cos and sin with alternate versions so that Maxima can’t simplify the expressions to cartesian form. I can then use ev(…,simp) to make use of simplification when comparing the expressions:

form_ans1:subst([cos=COSINE, sin=SINE], ans1);
form_ta1:subst([cos=COSINE, sin=SINE], ta1);
proper_form:is(ev(expand(form_ans1-form_ta1),simp)=0);

This will ensure that COSINE(pi/3) and COSINE((1/3)*pi) will cancel out, thanks to the simplification being turned on.

But since Maxima doesn’t know anything about COSINE, it can’t cancel out COSINE(-pi/3) and COSINE(5pi/3) (as it would do with cos) if students give their answer with the wrong value for the principal argument.

It was then just a case of replacing the test for EqualComAss(ans1,ta1) in the PRT with a test that AlgEquiv(proper_form, true), and regrading. Out of ~160 attempts this picked up 8 students who deserved full marks!

Update (08/11/2021): One year on, and STACK now has a new feature which makes it easier to grade these answers correctly! The new EqualComAssRules answer test lets you add a list of different algebraic rules so that two answers should count as equivalent if they differ only by those rules – e.g. x and 1*x.

To fix this question, it’s enough to change the first PRT node to the following, using the “Test options” box to specify the list of algebraic rules:

ATEqualComAssRules(ans1, ta1, [ID_TRANS,NEG_TRANS,DIV_TRANS,INT_ARITH]);