Formulation of Renormalization Group (RG) for turbulence: 2
In last week’s post, we recognised that the basic step of averaging over high-frequency modes was impossible in principle for a classical, deterministic problem such as turbulence. Curiously enough, for many years it has been recognized in the analogous subgrid modelling problem that a conditional average is required; and that this must be evaluated approximately. But even then it has not apparently been realised that the formulation of the average must also be approximate. As for theoretical physicists, they have long forgotten that Wilson pointed out the need for a conditional average in RG, and that it is evaded in their field by working with Gaussian distributions, which render it trivial. So one still sees the occasional pointless paper claiming to be a theory of turbulence by people who are unaware of the work of Forster et al as mentioned in my previous post.
During the second half of the 1980s, I was writing my first book on turbulence and simultaneously trying to figure out what was wrong with my iterative averaging form of RG. By the end of that decade I had sent off my MS to the publishers and could concentrate on the problems of RG. Early in 1990 I realised that the average over the ![]() could not be simply a filtered average if
could not be simply a filtered average if ![]() was to be held constant. Working closely with my student Alex Watt, I came up with the two-field theory to evaluate the conditional average approximately; and this produced a considerable improvement by reducing the dependence on the choice of spatial rescaling factor [1]. Early in 1991, when I returned from the US where I had visited MSRI, Berkeley, with a side visit to the Turbulence Centre at Stanford, we began work on a formulation of the conditional average, in which we were joined by another of my students, Bill Roberts. Some questions had arisen during my trip to the States and that lent additional impetus to this work. If memory serves, the key realisation that a conditional average of the type we were using was impossible for a macroscopic deterministic system was due to Alex and Bill; and arose when they were discussing this by themselves. This galvanised our approach and this work was published as reference [2].
was to be held constant. Working closely with my student Alex Watt, I came up with the two-field theory to evaluate the conditional average approximately; and this produced a considerable improvement by reducing the dependence on the choice of spatial rescaling factor [1]. Early in 1991, when I returned from the US where I had visited MSRI, Berkeley, with a side visit to the Turbulence Centre at Stanford, we began work on a formulation of the conditional average, in which we were joined by another of my students, Bill Roberts. Some questions had arisen during my trip to the States and that lent additional impetus to this work. If memory serves, the key realisation that a conditional average of the type we were using was impossible for a macroscopic deterministic system was due to Alex and Bill; and arose when they were discussing this by themselves. This galvanised our approach and this work was published as reference [2].
Although it defies chronology, we will discuss this theory first. Consider a set of realizations ![]() , with their low-
, with their low-![]() parts clustering around one particular member of the set
parts clustering around one particular member of the set ![]() , such that
, such that
![]()
where ![]() is the control parameter for the conditional average
is the control parameter for the conditional average ![]() and is chosen to satisfy
and is chosen to satisfy
![]()
In principle bounds on ![]() can be determined from a predictability study of the NSE, but clearly the more chaotic it is, the smaller is
can be determined from a predictability study of the NSE, but clearly the more chaotic it is, the smaller is ![]() , and of course when the conditional average is of modes with asymptotic freedom,
, and of course when the conditional average is of modes with asymptotic freedom, ![]() .
.
The two-field theory was put forward in [1] and the essential step was to write the high-![]() modes in terms of a new field
modes in terms of a new field ![]() , thus
, thus
![]()
Here ![]() is of the same general type as
is of the same general type as ![]() but is not coupled to
but is not coupled to ![]() . We identified a form for
. We identified a form for ![]() by making an expansion of the velocity field in Taylor series in wavenumber about
by making an expansion of the velocity field in Taylor series in wavenumber about ![]() . We tested the theory by predicting a value for
. We tested the theory by predicting a value for ![]() , the pre-factor in the Kolmogorov spectrum and found this to be much less sensitive to the value of the bandwidth parameter. This theory involved two plausible approximations and these were later subsumed into a consistent perturbation expansion in powers of the local (in wavenumber) Reynolds number, along with the expansion of the chaotic velocity field being replaced by an equivalent expansion of the covariance. The current situation is that we predict
, the pre-factor in the Kolmogorov spectrum and found this to be much less sensitive to the value of the bandwidth parameter. This theory involved two plausible approximations and these were later subsumed into a consistent perturbation expansion in powers of the local (in wavenumber) Reynolds number, along with the expansion of the chaotic velocity field being replaced by an equivalent expansion of the covariance. The current situation is that we predict ![]() over the range
over the range ![]() of the bandwidth parameter. Evidently this breaks down for
of the bandwidth parameter. Evidently this breaks down for ![]() as the band is so small that integrals are dominated by behaviour near the lower cut-off wavenumber; while for
as the band is so small that integrals are dominated by behaviour near the lower cut-off wavenumber; while for ![]() the breakdown is due to the inadequacy of the first-order truncation of the Taylor series for a large bandwidth.
the breakdown is due to the inadequacy of the first-order truncation of the Taylor series for a large bandwidth.
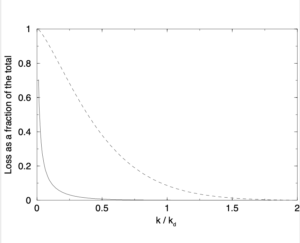
In carrying out this analysis, we eliminate modes starting from a maximum value of ![]() and end up with the onset of scale-invariance at a fixed-point wavenumber which is a fraction of
and end up with the onset of scale-invariance at a fixed-point wavenumber which is a fraction of ![]() . This fixed point is the top of the inertial range of wavenumbers and, although this is not a precisely defined wavenumber, experimentalists have traditionally taken it to be
. This fixed point is the top of the inertial range of wavenumbers and, although this is not a precisely defined wavenumber, experimentalists have traditionally taken it to be ![]() , where
, where ![]() is the Kolmogorov wavenumber. If we take
is the Kolmogorov wavenumber. If we take ![]() (see the figure which is taken from reference [4]) and consider the case
(see the figure which is taken from reference [4]) and consider the case ![]() , where the fixed point occurs at the fourth iteration, we find the numerical value of the fixed-point wavenumber is
, where the fixed point occurs at the fourth iteration, we find the numerical value of the fixed-point wavenumber is ![]() , in pretty good agreement with the experimental picture.
, in pretty good agreement with the experimental picture.
To sum up, this method seems to represent the inertial transfer of energy rather well. But, as it stands, if offers nothing on the phase-coupling effects in the momentum equations which are usually referred to as eddy noise.
[1] W. D. McComb and A. G. Watt. Conditional averaging procedure for the elimination of the small-scale modes from incompressible-fluid turbulence at high Reynolds numbers. Phys. Rev. Lett., 65(26):3281-3284, 1990.
[2] W. D. McComb, W. Roberts, and A. G. Watt. Conditional-averaging procedure for problems with mode-mode coupling. Phys. Rev. A, 45(6):3507-3515, 1992.
[3] W. D. McComb and A. G. Watt. Two-field theory of incompressible-fluid turbulence. Phys. Rev. A, 46(8):4797-4812, 1992.
[4] W. D. McComb, A. Hunter, and C. Johnston. Conditional mode-elimination and the subgrid-modelling problem for isotropic turbulence. Phys. Fluids, 13:2030, 2001.



