How can we reduce the number of degrees of freedom necessary for a turbulence calculation?
This question first arose in the 1960s with attempts to do meteorological simulations. The response was Large Eddy Simulation (LES), with its associated sub-grid modelling. A short introduction to this topic can be found in section 3.1 of the book [1] with a longer treatment in chapter 10 of the same reference. A more fundamental approach was introduced with the work of Kraichnan [2] in 1976 who applied his test field model to calculate an effective viscosity to represent the sub-grid flux in isotropic turbulence. This resulted in the well-known ‘plateau and peak’ form; but, having been derived from a statistical theory, it could not represent the phase effects of the random velocity field.
In a series of papers, beginning in 1990, McComb, Roberts and Watt introduced the iterative conditional averaging method to calculate a sub-grid viscosity for isotropic turbulence [3–5]. This method is the only use of the renormalization group algorithm that takes account of the differences between classical fluid turbulence and quantum field theory or the theory of critical phenomena. The resulting sub-grid viscosity takes good account of the inertial energy transfer to the sub-grid modes but does not fully represent the phase effects.
Lastly, the operational method of Young and McComb [6,7] used a feedback loop to modify the velocity field to ensure the correct monotonic decline of the energy spectrum. Good results are obtained, and phase effects are fully taken into account.
However, none of these methods retains all the degrees of freedom. For isotropic turbulence, these are the Fourier components of the velocity field, and referring to [1] page 113, we have:
(1) 
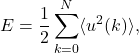
where 
is the total kinetic energy per unit mass of the turbulence. The total number of degrees of freedom 
can be shown to depend on the Reynolds number to the power of 
, and so increases rapidly with increasing Reynolds number. Accordingly, the price one pays for reducing the number of degrees of freedom while still representing the dissipation rate correctly means that in principle and practice there must be some reduction of the total kinetic energy. This may not be too serious a matter: see the figure 2 in reference [8]. Here we see that the maximum resolved wavenumber must be greater than 
, where 
is the Kolmogorov dissipation wavenumber; whereas the total energy may be represented with a maximum resolved wave number of less then 
. It should be noted that this graph is based on a particular model spectrum, but similar results would be achieved with other model spectra or indeed with the results of numerical simulation.
This year a new method has been a proposed by Donzis and Sanjeev which reduces the computational effort but still retains all the degrees of freedom [9]. In this method, all the degrees of freedom are divided at the time step 
into resolved modes, which are integrated forward in time to 
using the NSE; and unresolved modes which are assumed not to change at that time step. The resolved modes are selected by a random sampling process which is carried out at each time step. In this way, the total number of degrees of freedom remains the same, but those actually being computed differ from one time step to another. The method was investigated for two different sampling criteria and for different fractions of the total number of modes being resolved, ranging from 10% to 100% (corresponding to full simulation), with impressive qualitative and quantitative results for energy spectra, dissipation rate, skewness and so on. This seems to be a promising method of numerical simulation, but also promises to shed light on the nature of turbulence.
[1] W. D. McComb. The Physics of Fluid Turbulence. Oxford University Press, 1990.
[2] R. H. Kraichnan. Eddy-viscosity in two and three dimensions. J. Atmos.Sci., 33:1521, 1976.
[3] W. D. McComb and A. G. Watt. Conditional averaging procedure for the elimination of the small-scale modes from incompressible fluid turbulence at high Reynolds numbers. Phys. Rev. Lett., 65(26):3281–3284, 1990.
[4] W. D. McComb, W. Roberts, and A. G. Watt. Conditional-averaging procedure for problems with mode-mode coupling. Phys. Rev. A, 45(6):3507–3515, 1992.
[5] W. D. McComb and A. G. Watt. Two-field theory of incompressible-fluid turbulence. Phys. Rev. A, 46(8):4797–4812, 1992.
[6] W. D. McComb and A. J. Young. Explicit-Scales Projections of the Partitioned Nonlinear Term in Direct Numerical Simulation of the Navier-Stoke Equation. Presented at 2nd Monte Verita Colloquium on Fundamental Prob-lematic Issues in Turbulence: available at ArXiV:physics/9806029 v1, 1998.
[7] A. J. Young and W. D. McComb. Effective viscosity due to local turbulence interactions near the cutoff wavenumber in a constrained numerical simulation. J. Phys. A, 33:133–139, 2000.
[8] W. D. McComb, A. Hunter, and C. Johnston. Conditional mode-elimination and the subgrid-modelling problem for isotropic turbulence. Phys. Fluids, 13:2030, 2001.
[9] Diego Donzis and Shilpa Sajeev. Degrees of freedom and the dynamics of fully developed turbulence. Physical Review Fluids, 9:044605–1–11, 2024.
