image_pdfimage_print

The modified Lin equation.

In my post of 27 February I discussed the importance of being aware of the full form of the Lin equation as this reveals the existence of a cascade in wavenumber space. In this post I want to take this a bit further, using my resolution of the scale-invariance paradox [1].

For me this topic first arose during a meeting in 1991 at MSRI, Berkeley. When I had finished my talk, Bob Kraichnan came up to me with a copy of my recently published book and pointed out Figure 2.5, which was a plot of the terms in the Lin equation for freely decaying turbulence. He commented on the fact that the transfer spectrum T(k) was shown as zero for an extended range of values of k. He commented that people used to think that was the case, because it would be expected from the scale-invariance of the flux, but that in practice it was never observed. There was always a single zero-crossing. I was able to reassure him that figure was based on a computation of the LET theory; that there had been an error which had now been rectified; and that the revised figure would show a single zero-crossing and would appear in the paperback edition of the book to be published later that year.

However, I was left with a nagging feeling that there was an unresolved problem with this result. The first measurements of T(k) had been published by Uberoi [2] in 1963, and this author had said that the single zero-crossing was probably due to the low Reynolds number and indicated that he would expect T(k)=0 over an extended range of k to develop with increasing Reynolds number. Although this does not seem to have been a matter of widespread concern, over the 1970s/80s/90s various ad hoc methods were used to cope with this behaviour in numerical calculations: for some references to this work, see [1]. As a matter of interest, I include both versions of Figure 2.5 below.

Figure 2.5 from Physics of Fluid Turbulence 1990
Figure 2.5 from Physics of Fluid Turbulence 1991

 

 

 

 

 

 

 

 

 

 

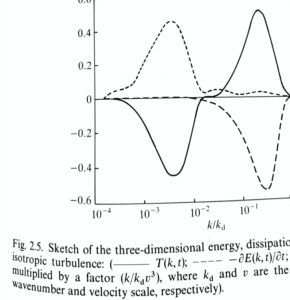
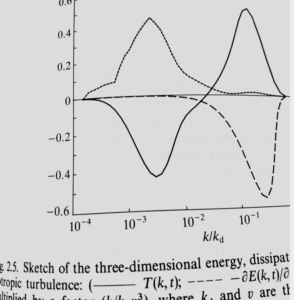
The Lin equation (see reference [3]) takes the form:

(1)   \begin{equation*} \left( \frac{d}{dt} + 2 \nu k^2 \right) E(k,t) = T(k,t)\end{equation*}

where E(k,t) is the energy spectrum, T(k,t) is the energy transfer spectrum and \nu is the kinematic viscosity. Now let us integrate each term of (1) with respect to wavenumber, from zero up to some arbitrarily chosen wavenumber \kappa:

(2)   \begin{equation*} \frac{d}{dt}\int_{0}^{\kappa} dk\, E(k,t) = \int^{\kappa}_{0} dk\, T(k,t)-2 \nu\int_{0}^{\kappa} dk\, k^2 E(k,t). \end{equation*}

The energy transfer spectrum may be written as

(3)   \begin{equation*} T(k,t) = \int^{\infty}_{0} dj\, S(k,j;t), \end{equation*}

where, as is well known, S(k,j;t) can be expressed in terms of the triple moment. Its antisymmetry under interchange of k and j guarantees energy conservation in the form:

(4)   \begin{equation*}\int^{\infty}_{0} dk\, T(k,t) =0. \end{equation*}

With some use of the antisymmetry of S, along with equation (4), equation (2) may be written as

(5)   \begin{equation*}\frac{d}{dt}\int_{0}^{\kappa} dk\, E(k,t) = - \int^{\infty}_{\kappa} dk\,\int^{\kappa}_{0} dj\, S(k,j;t)-2 \nu\int_{0}^{\kappa} dk\, k^2 E(k,t).\end{equation*}

the integral of the transfer term is readily interpreted as the net flux of energy from wavenumbers less than \kappa to those greater than \kappa, at any time t.

It is convenient to introduce a specific symbol \Pi for this energy flux, thus:

(6)   \begin{equation*}\Pi (\kappa,t) = \int^{\infty}_{\kappa} dk\, T(k,t) =-\int^{\kappa}_{0} dk\,T(k,t),\end{equation*}

where the second equality follows from (4).

The key to resolving the paradox is to introduce transfer spectra which have been filtered with respect to k and which have had their integration over j partitioned at the filter cut-off, i.e. j=k_c [1],[4]. Beginning with the Heaviside unit step function, defined by:

(7)   \begin{eqnarray*} H(x) & = & 1 \qquad \mbox{for} \qquad x > 0; \\& = & 0 \qquad \mbox {for} \qquad x < 0.\end{eqnarray*}

we may define low-pass and high-pass filter functions, thus:

(8)   \begin{equation*}\theta^{-}(x) = 1 - H(x),\end{equation*}

and

(9)   \begin{equation*} \theta^{+}(x) = H(x). \end{equation*}

We may then decompose the transfer spectrum, as given by (3), into four constituent parts,

(10)   \begin{equation*}T^{--}(k|k_{c}) = \theta^{-}(k-k_{c})\int^{k_{c}}_{0}dj\, S(k,j); \end{equation*}

(11)   \begin{equation*} T^{-+}(k|k_{c}) = \theta^{-}(k-k_{c})\int^{\infty}_{k_{c}}dj\, S(k,j); \end{equation*}

(12)   \begin{equation*} T^{+-}(k|k_{c}) = \theta^{+}(k-k_{c})\int^{k_{c}}_{0}dj\, S(k,j); \end{equation*}

and

(13)   \begin{equation*}T^{++}(k|k_{c}) = \theta^{+}(k-k_{c})\int^{\infty}_{k_{c}}dj\, S(k,j), \end{equation*}

such that the overall requirement of energy conservation is satisfied:

(14)   \begin{equation*} \int^{\infty}_{0}dk\left[T^{--}(k|k_{c}) + T^{-+}(k|k_{c}) + T^{+-}(k|k_{c}) + T^{++}(k|k_{c})\right] = 0. \end{equation*}

It is readily verified that the individual filtered/partitioned transfer spectra have the following properties:

(15)   \begin{equation*} \int^{k_{c}}_{0}dk\, T^{--}(k|k_{c}) = 0; \end{equation*}

(16)   \begin{equation*} \int^{k_{c}}_{0}dk\, T^{-+}(k|k_{c}) = -\Pi(k_{c}); \end{equation*}

(17)   \begin{equation*}\int^{\infty}_{k_{c}}dk\, T^{+-}(k|k_{c}) = \Pi(k_{c}); \end{equation*}

and

(18)   \begin{equation*} \int^{\infty}_{k_{c}}dk\, T^{++}(k|k_{c}) = 0. \end{equation*}

Equation (2) may be rewritten in terms of the filtered/partitioned transfer spectrum as:

(19)   \begin{equation*} \frac{d}{dt}\int^{k_{c}}_{0}dk\, E(k,t) = -\int^{\infty}_{k_{c}}dk\, T^{+-}(k|k_{c}) -2\nu_{0}\int^{k_{c}}_{0}dk\, k^{2}E(k,t). \end{equation*}

We note from equation (15) that T^{--}(k|k_c) is conservative on the interval [0,k_c], and hence does not appear in (19), while T^{-+}(k|k_{c}) has been replaced by -T^{+-}(k|k_{c}), using (16) and (17). Those working with DNS or analytical theory, can avoid the paradox by changing their definition of energy fluxes, from those given by (6), to the forms:

(20)   \begin{equation*} \Pi (\kappa,t) = \int^{\infty}_{\kappa} dk\, T^{+-}(k|\kappa,t) =-\int^{\kappa}_{0} dk\, T^{-+}(k|\kappa,t), \end{equation*}

where T^{+-}(k|\kappa,t) is defined by (12) and T^{-+}(k|\kappa,t) by (11). This is equivalent to (6); but, unlike it, avoids the paradox.

This behaviour is illustrated in the figure below, where we should note that T^{-+}(k|\kappa) is defined below the cut-off wavenumber \kappa = k_{c}, and -T^{+-}(k|\kappa) is defined above it.

 

Modified form of transfer spectrum to avoid the scale-invariance paradox.

 

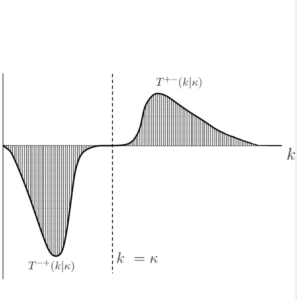
This raises the question of how exactly the Lin equation should be written, in order to emphasise these properties. That will be the subject of a paper which is now in preparation [5]. It is worth making the point that the filtered-partitioned forms of the transfer spectrum have only been studied in the context of the subgrid modelling problem [4]. Given the much more powerful computers now available, it would undoubtedly be rewarding to study the role of these terms in the energy balance for a range of Reynolds numbers. I very much hope that someone will do this.

Acknowledgement: the above figure was suggested by John Morgan, who also prepared it.

[1] David McComb. Scale-invariance in three-dimensional turbulence: a paradox and its resolution. J. Phys. A: Math. Theor., 41:75501, 2008.
[2] M. S. Uberoi. Energy transfer in isotropic turbulence. Phys. Fluids, 6:1048, 1963.
[3] W. David McComb. Homogeneous, Isotropic Turbulence: Phenomenology, Renormalization and Statistical Closures. Oxford University Press, 2014.
[4] W. D. McComb and A. J. Young. Explicit-Scales Projections of the Partitioned Nonlinear Term in Direct Numerical Simulation of the Navier-Stokes Equation. In Proc. 2nd Monte Verita Colloquium on Fundamental Problematic Issues in Turbulence: available at arXiv:physics/9806029 v1, 1998.
[5] W. D. McComb. A modified Lin equation for the energy balance in isotropic turbulence. arXiv:2007.13622v1 [physics.flu-dyn] 27 Jul 2020

 

 

 

 

 

 

The modified Lin equation. / David McComb on the Physics of Turbulence by blogadmin is licensed under a Creative Commons Attribution CC BY 3.0

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.