The non-Markovian nature of turbulence 6: the assumptions that led to the Edwards theory being Markovian.
Turbulence theories are usually referred to by acronyms e.g. DIA, SCF, ALHDIA, \dots, and so on. Here SCF is Herring’s theory and, to avoid confusion, Herring and Kraichnan referred to the Edwards SCF as EDW [1]. Later on, when I came to write my first book on turbulence [2], I referred to it as EFP, standing for `Edwards-Fokker-Planck’ theory. This seemed appropriate as Edwards was guided by the theory of Brownian motion. But it did not occur to me at the time that the significance of this was that his theory was Markovian with respect to interactions in wavenumber space; nor indeed that a Markovian form was the common denominator in all three of the pioneering Eulerian theories. In recent years, it did occur to me that it was not necessary to be so prescriptive; and if one took a less constrained approach the result was a non-Markovian theory, in fact the LET theory.
Following Edwards [3], we define a model system in terms of a Gaussian distribution ![]() , which is chosen such that it is normalised to unity and recovers the exact covariance. That is:
, which is chosen such that it is normalised to unity and recovers the exact covariance. That is:
(1) ![]()
and
(2) ![]()
respectively. Then one solves the Liouville equation for the exact probability distribution in terms of a perturbation series with ![]() as the zero-order term. We will not go into further details here, as we just want to understand how the Edwards theory was constrained to give a Markovian form.
as the zero-order term. We will not go into further details here, as we just want to understand how the Edwards theory was constrained to give a Markovian form.
Equations (1) and (2) introduce the two-time covariance. However, in order to explain the Edwards theory, we will consider the single-time case. Also, for sake of simplicity, we will employ the reduced notation of Herring, as used extensively by Leslie [4] and others (see [2]). In this notation we represent the velocity field by ![]() , where the index is a combined wave-vector and cartesian tensor index (i.e our
, where the index is a combined wave-vector and cartesian tensor index (i.e our ![]() and
and ![]() ). Accordingly, we introduce the Edwards-Fokker-Planck operator as the sum of single-mode operators, in the form:
). Accordingly, we introduce the Edwards-Fokker-Planck operator as the sum of single-mode operators, in the form:
(3) ![]()
where ![]() is a renormalized eddy decay rate and
is a renormalized eddy decay rate and ![]() is the covariance of the velocity field, such that
is the covariance of the velocity field, such that
(4) ![]()
and ![]() is the exact distribution. Then it is readily verified that the model equation:
is the exact distribution. Then it is readily verified that the model equation:
(5) ![]()
has the Gaussian solution
(6) 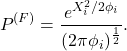
However, it is important to note, and is also readily verified, that a more general form of the operator ![]() , which is given by
, which is given by
(7) ![]()
where ![]() is an arbitrarily chosen well behaved function, also yields the same Gaussian solution for the zero-order equation:
is an arbitrarily chosen well behaved function, also yields the same Gaussian solution for the zero-order equation:
(8) ![]()
Hence at this stage the operator ![]() is not fully determined. Edwards was guided by an analogy with the theory of Brownian motion and in effect made the choice
is not fully determined. Edwards was guided by an analogy with the theory of Brownian motion and in effect made the choice
(9) ![]()
in order to generate a base operator which could be inverted in terms of an eigenfunction expansion of Hermite polynomials. In this process, the ![]() appeared as eigenvalues.
appeared as eigenvalues.
It is this specific choice which over-determines the basic operator which constrained the Edwards theory to be Markovian. More recently it was found that a more minimalist choice, allied to a two-time representation, leads formally to the LET theory [5]. We will consider a more physical basis for the LET theory in the next post.
[1] J. R. Herring and R. H. Kraichnan. Comparison of some approximations for isotropic turbulence Lecture Notes in Physics, volume 12, chapter Statistical Models and Turbulence, page 148. Springer, Berlin, 1972.
[2] W. D. McComb. The Physics of Fluid Turbulence. Oxford University Press, 1990.
[3] S. F. Edwards. The statistical dynamics of homogeneous turbulence. J. Fluid Mech., 18:239, 1964.
[4] D. C. Leslie. Developments in the theory of turbulence. Clarendon Press, Oxford, 1973.
[5] W. D. McComb and S. R. Yoffe. A formal derivation of the local energy transfer (LET) theory of homogeneous turbulence. J. Phys. A: Math. Theor., 50:375501, 2017



