Turbulence renormalization and the Euler equation: 4
In the previous post we mentioned that Kraichnan’s DIA theory [1] and Wyld’s [2] diagrammatic formalism both depended on the use of an externally applied stirring force to define the response function. This is also true of the later functional formalism of Martin, Siggia and Rose [3]. Both formalisms agree with DIA at second order, and a general discussion of these matters can be found in references [4] and [5]. We also pointed out that this use of applied forces poses problems for the Euler equation. This is because the absence of viscosity means that the kinetic energy will increase without limit. That of course is the reason why numerical studies are limited to the spectrally truncated Euler equation, where the modes are restricted to 
. So the fact that the Euler equation can behave like the Navier-Stokes equation (NSE) in a transient way not only raises questions about the interpretation of renormalized perturbation theory (RPT) as a renormalization of the molecular viscosity, it also raises doubts about the use of external forces to develop the RPT in the first place.
In the investigations of Cichowlas \emph{et al} [6] and Bos and Bertoglio [7], as discussed in the first of this series of posts on 19 May, the system was given a finite amount of energy which it then redistributed among the modes. For modes with 
, an NSE-like cascade was observed, with a Kolmogorov spectrum; while for 
the 
equipartition spectrum was observed. Obviously, in the absence of viscosity the total energy is constant and the system must move to equipartition for all values of wavenumber. Thus the value of 
separating the two forms of behaviour must tend to zero in, it is reasonable to assume, a finite time.
If we applied stirring forces to the spectrally truncated Euler equation, such that they constituted an energy input at low modes at a rate 
, then in the absence of viscosity this could be balanced by a form of dissipation to the equipartition modes, where the energy contained in these modes is given by
(1) 
and the dissipation rate by
(2) 
as discussed in reference [6]. Evidently as time goes on, will decrease to some minimum value, which would be determined by the peakiness of the input spectrum near the origin, and after that the total energy would increase without limit.
The only way one could maintain a quasi-NSE form of behaviour in the presence of an input term would be by increasing the value of 
and ultimately taking 
. This naturally rules out numerical simulation but possibly some form of limit could be investigated numerically, rather as the infinite Reynolds number limit can be established in numerical simulations. Cichowlas \emph{et al} [6] introduced an analogue of the Kolmogorov dissipation wavenumber 
such that
(3) 
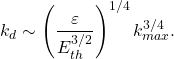
This raises the possibility that taking the limit of 
would correspond to the infinite Reynolds number limit which is 
such that 
, leading to 
I will extend the discussion to the use of Renormalization Group (RG) in the next post. In the meantime, for sake of completeness I should mention that there is a school of activity in which RPTs are derived in Lagrangian coordinates. The latest developments in this area, along with a good discussion of its relationship to Eulerian theories, can be found in the paper by Okamura [8].
[1] R. H. Kraichnan. The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech., 5:497{543, 1959.
[2] H. W. Wyld Jr. Formulation of the theory of turbulence in an incompressible fluid. Ann.Phys, 14:143, 1961.
[3] P. C. Martin, E. D. Siggia, and H. A. Rose. Statistical Dynamics of Classical Systems. Phys. Rev. A, 8(1):423-437, 1973.
[4] A. Berera, M. Salewski, and W. D. McComb. Eulerian Field-Theoretic Closure Formalisms for Fluid Turbulence. Phys. Rev. E, 87:013007-1-25, 2013.
[5] W. D. McComb. The Physics of Fluid Turbulence. Oxford University Press, 1990.
[6] Cyril Cichowlas, Pauline Bonatti, Fabrice Debbasch, and Marc Brachet. Effective Dissipation and Turbulence in Spectrally Truncated Euler Flows. Phys. Rev. Lett., 95:264502, 2005.
[7] W. J. T. Bos and J.-P. Bertoglio. Dynamics of spectrally truncated inviscid turbulence. Phys. Fluids, 18:071701, 2006.
[8] Makoto Okamura. Closure model for homogeneous isotropic turbulence in the Lagrangian specification of the flow field. J. Fluid Mech., 841:133, 2018.
