image_pdfimage_print

The Kolmogorov-Obukhov Spectrum.

To lay a foundation for the present piece, we will first consider the joint Kolmogorov-Obukhov picture in more detail. For completeness, we should begin by mentioning that Kolmogorov also used the Karman-Howarth equation, which is the energy balance equation connecting the second- and third-order structure functions, to derive the so-called `4/5‘ law for the third-order structure function.This procedure amounts to a de facto closure, as the time-derivative is neglected (an exact step in our present case, as we are restricting our attention to stationary turbulence) and the term involving the viscosity vanishes in the limit of infinite Reynolds number. This is often referred to as `the only exact result in turbulence theory’; but increasingly it is being referred to, perhaps more correctly, as `the only asymptotically exact result in turbulence’.

As part of this work, he also assumed that the skewness was constant; and this provided a relationship between the second- and third-order structure functions which recovered the `2/3‘ law. It is interesting to note that Lundgren used the method of matched asymptotic expansions to obtain both the `4/5‘ and `2/3‘ laws, without having to make any assumption about the skewness. This work also offered a way of estimating the extent of the inertial range in real space.

However, the Karman-Howarth equation is local in the independent variables and therefore does not describe an energy cascade. In contrast, the Lin equation (which is just its Fourier transform) shows that all the degrees of freedom in turbulence are coupled together. It takes the form, for the energy spectrum E(k, t), in the presence of an input spectrum W(k):

(1)   \begin{equation*}\frac{\partial E(k,t)}{\partial t} = W(k)+ T(k,t)- 2\nu_{0}k^{2}E(k, t),\end{equation*}

where \nu_{0} is the kinematic viscosity and the transfer spectrum T(k,t) is given by

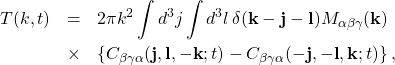
(2)   \begin{eqnarray*}T(k,t) & = & 2\pi k^{2}\int d^{3}j\int d^{3}l\,\delta(\mathbf{k}-\mathbf{j}-\mathbf{l})M_{\alpha\beta\gamma}(\mathbf{k})\nonumber \\ & \times & \left\{C_{\beta\gamma\alpha}(\mathbf{j},\mathbf{l},\mathbf{-k};t)-C_{\beta\gamma\alpha}(\mathbf{-j},\mathbf{-l},\mathbf{k};t)\right\},\end{eqnarray*}

with

(3)   \begin{equation*} M_{\alpha\beta\gamma}(\mathbf{k})=-\frac{i}{2}\left[k_{\beta}P_{\alpha\gamma}(\mathbf{k})+k_{\gamma}P_{\alpha\beta}(\mathbf{k})\right],\end{equation*}

and the projector P_{\alpha\beta}(\mathbf{k}) is

(4)   \begin{equation*}P_{\alpha\beta}(\mathbf{k})=\delta_{\alpha\beta}-\frac{k_{\alpha}k_{\beta}}{|\mathbf{k}|^{2}}, \end{equation*}

where \delta_{\alpha\beta} is the Kronecker delta, and the third-order moment C_{\beta\gamma\alpha} here takes the specific form:

(5)   \begin{equation*} C_{\beta\gamma\alpha}(\mathbf{j},\mathbf{l},\mathbf{-k};t)=\langle u_{\beta}(\mathbf{j},t)u_{\gamma}(\mathbf{l},t)u_{\alpha}(\mathbf{-k},t) \rangle.\end{equation*}

At this stage we also define the flux of energy \Pi(\kappa,t) due to inertial transfer through the mode with wavenumber k=\kappa. This is given by:

(6)   \begin{equation*}\Pi(\kappa,t) = \int_{\kappa}^{\infty}\,dk\,T(k,t).\end{equation*}

Further discussion and details may be found in Section 4.2 of the book [1].
We now have a rather simple picture. In formulating our problem, the shape of the input spectrum should be chosen to be peaked near the origin, such that higher wavenumbers are driven by inertial transfer, with energy being dissipated locally by the viscosity. Then we can define the rate at which stirring forces do work on the system by:

(7)   \begin{equation*} \int_0^\infty \, W(k)\, dk = \varepsilon_W. \end{equation*}

Obukhov’s idea of the constant inertial flux can be expressed as follows. As the Reynolds number is increased, the transfer rate, as given by equation (6), will also increase and must reach a maximum value, which in turn must be equal to the viscous dissipation. Thus we introduce the symbol \varepsilon_T for the maximum inertial flux as:

(8)   \begin{equation*}\varepsilon_T = \Pi_{\mbox{max}},\end{equation*}

and for stationary turbulence at sufficiently high Reynolds number, we have the limiting condition:

(9)   \begin{equation*}\varepsilon = \varepsilon_T = \varepsilon_W.\end{equation*}

Thus the loose idea of a local cascade involving eddies in real space is replaced by the precisely formulated concept of scale invariance of the inertial flux in wavenumber space. As is well known, this picture leads directly to the -5/3 energy spectrum in the limit of large Reynolds numbers.

[1] W. David McComb. Homogeneous, Isotropic Turbulence: Phenomenology, Renormalization and Statistical Closures. Oxford University Press, 2014.

The Kolmogorov-Obukhov Spectrum. / David McComb on the Physics of Turbulence by blogadmin is licensed under a Creative Commons Attribution CC BY 3.0

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.