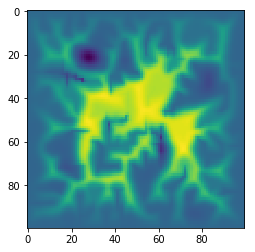
In my spare time, I completed a pretty cool erosion function which I would like to keep. It looks like this:

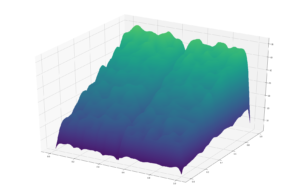
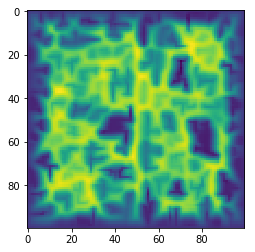
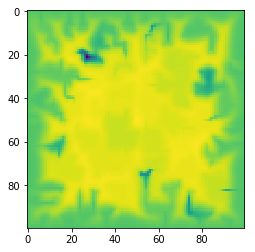
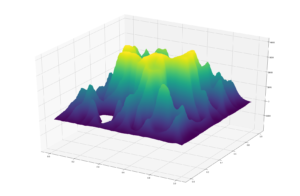
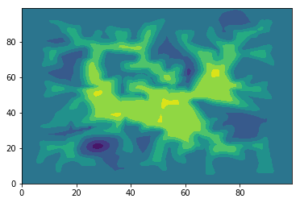
It features a wind/elements based approach which acts to smooth the surface, alongside a rivers-based approach which creates the channels. together they create very realistic models of different features!

This is the river model, and the terrain it is acting on;

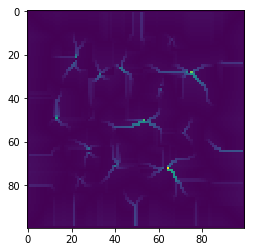
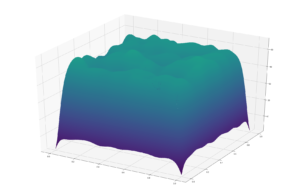
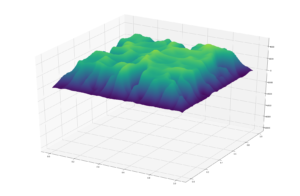
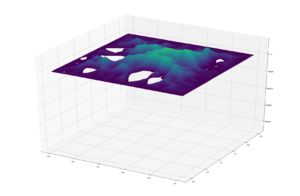
These are some examples of erosion creating flat:

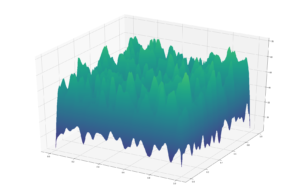
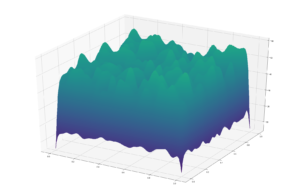
and the rest are all images with different random seeds. Very happy with it!

def depo_func(J):
##takes an array of terrain heights and returns the deposition rate
J=np.array(J)
x1=[]
X0=[]
for i in range(len(J)):
for j in range(len(J[0])):
x=[]
if i==0:
x.append(0)
if j==0:
x.append(0)
x.append(J[1,0])
x.append(J[0,1])
elif j==len(J)-1:
x.append(0)
x.append(J[0,j-1])
x.append(J[1,j])
else:
x.append(J[0,j-1])
x.append(J[0,j+1])
x.append(J[1,j])
elif i==len(J)-1:
x.append(0)
if j==0:
x.append(0)
x.append(J[i-1,0])
x.append(J[i,1])
elif j==len(J)-1:
x.append(0)
x.append(J[i,j-1])
x.append(J[i-1,j])
else:
x.append(J[i,j-1])
x.append(J[i,j+1])
x.append(J[i-1,j])
elif j==0:
x.append(0)
x.append(J[i-1,0])
x.append(J[i+1,0])
x.append(J[i,1])
elif j==len(J)-1:
x.append(0)
x.append(J[i-1,j])
x.append(J[i+1,j])
x.append(J[i,j-1])
else:
x.append(J[i,j+1])
x.append(J[i+1,j])
x.append(J[i,j-1])
x.append(J[i-1,j])
X=np.mean(x)
X= X-J[i,j]
X0.append(X)
x1.append(X0)
X0=[]
return(x1)

def erosion_func(J,erosion_rate):
##takes an array of terrain heights and returns the eroded landscape
x1=depo_func(J)
x1=np.array(x1)
J=np.array(J)

o=[]
O=[]

for i in range(len(J)):
for j in range(len(J[0])):
o.append(J[i,j]+x1[i,j]*erosion_rate)
O.append(o)
o=[]
return(O)

def whichdirectionislowest(J,coordinate_storage):
###takes in location in array, and calculates coordinates of lowest neighbour
###returns new coordinates
J=np.array(J)
currentheight=J[coordinate_storage[0],coordinate_storage[1]]
if coordinate_storage[0]==0 or coordinate_storage[1]==0 or coordinate_storage[0]==len(J)-1 or coordinate_storage[1]==len(J)-1:
c=0
else:

removal=0#ticker as to whether we are on the bottom edge
##x is coordinate storage 0, y is coordinate storage 1

##choose the lowest number nearby
lowest=[]

#add 100*X1 to make sure it doesn’t refill places already full

row_1=J[coordinate_storage[0]-1]
row_2=J[coordinate_storage[0]]
row_3=J[coordinate_storage[0]+1]

lowest.append(row_1[coordinate_storage[1]])
lowest.append(row_2[coordinate_storage[1]+1])
lowest.append(row_2[coordinate_storage[1]-1])
lowest.append(row_3[coordinate_storage[1]])

if min(lowest)>currentheight:
c=0
elif lowest[0]==min(lowest):
coordinate_storage=[coordinate_storage[0]-1,coordinate_storage[1]]
elif lowest[1]==min(lowest):
coordinate_storage=[coordinate_storage[0],coordinate_storage[1]+1]
elif lowest[2]==min(lowest):
coordinate_storage=[coordinate_storage[0],coordinate_storage[1]-1]
elif lowest[3]==min(lowest):
coordinate_storage=[coordinate_storage[0]+1,coordinate_storage[1]]
lowest.append(currentheight)
currentheight=min(lowest)

return(coordinate_storage)

##execution

for i in range(100):
print(i)
J=erosion_func(J,0.2)
J=rivererosion(J,0.02)

plt.imshow(J)

plt.contourf(J)

Unrelated fun! / Space: weather or not by blogadmin is licensed under a Creative Commons Attribution CC BY 3.0