image_pdfimage_print

An assessment of Onsager’s concept of scale invariance: 1

We stated Onsager’s criterion [1] for an inertial range in terms of a scale-invariant flux as equation (4) in our post of 24 June 2024. In order to assess Onsager’s concept, we begin by considering the Lin equation in terms of the energy spectrum E(k,t) and the transfer spectrum T(k,t). We may write it in its well-known form:

(1)   \begin{equation*}\frac{d E(k,t)}{dt} = T(k,t) - 2\nu k^2E(k,t) \equiv T(k,t) - D(k,t),\end{equation*}

where D(k,t) is the energy dissipation spectrum, as given by D(k,t) = 2\nu k^{2}E(k,t). Here, we assume that there are no forces acting. We may also express the transfer spectrum in terms of its spectral density S(k,j;t) thus:

(2)   \begin{equation*} T(k,t) = \int_0^\infty\, dj \,S(k,j;t),\quad \mbox{where} \quad S(k,j;t) = -S(j,k;t);\end{equation*}

and S(k,j;t) contains the triple moment in wavenumber space: see [2]. Note that the antisymmetry of S(k,j;t) under the interchange of k and j guarantees that conservation of energy is maintained in the form \int_0^\infty\, dk T(k) = 0. When we substitute for T(k) in terms of S(k,j;t), we obtain the second form of the Lin equation.

If we write it in this, its full form, the Lin equation, tells us that all the Fourier modes are coupled to each other. It is, in the language of physics, an example of the many-body problem. It is in fact highly non-local, as in principle it couples every mode to every other mode. A corollary of this is that it predicts an energy cascade. This can be deduced from the nonlinear term which couples all modes together plus the presence of the viscous term which is symmetry-breaking. If the viscous term were set equal to zero, then the coupled but inviscid equation would yield equipartition states.

We may consider the transfer of energy from wavenumbers less than \kappa to wavenumbers greater than \kappa. To do this, we integrate the terms of the Lin equation from k=0 to an arbitarily chosen k=\kappa, with the result:

(3)   \begin{eqnarray*}\frac{d}{dt}\int^{\kappa}_{0}dk E(k,t) & = &\int_{0}^{\kappa}dk\int^{\infty}_{0}dj S(k,j;t)-\int^{\kappa}_{0}dk D(k,t) \nonumber \\& = & \int_{0}^{\kappa}dk\int^{\infty}_{\kappa}dj S(k,j;t)-\int^{\kappa}_{0}dk D(k,t),\end{eqnarray*}

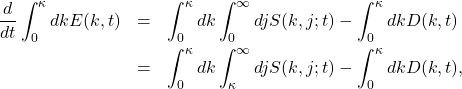
where the second form of the right hand side relies on the fact that the double integral over 0\leq k,j \leq \kappa vanishes due to the antisymmetry of S(k,j;t). Evidently this equation tells us that the loss of energy from modes with k\leq \kappa is due to transfer to modes with k\geq \kappa, as well as the direct loss to dissipation.

In order to consider the inertial transfer further, we first introduce the symbol E_{\kappa}(t) for the amount of energy contained in modes 0\leq k \leq \kappa, thus:

(4)   \begin{equation*}\frac{d}{dt}E_{\kappa}(t) = \frac{d}{dt}\int^{\kappa}_{0}dk E(k,t).\end{equation*}

We then introduce the symbol \Pi(\kappa,t), defined by:

(5)   \begin{equation*}\Pi(\kappa,t) = \int^{\infty}_{\kappa}dk T(k,t) = -\int^{\kappa}_{0}dk T(k,t)\end{equation*}

which represents the flux through mode k=\kappa; and, in terms of the transfer spectral density,

(6)   \begin{equation*} \Pi(\kappa,t) = \int^{\infty}_{\kappa}dk\int^{\kappa}_{0}dj\,S(k,j;t) = -\int^{\kappa}_{0}dk\int^{\infty}_{\kappa}dj\, S(k,j;t).\end{equation*}

Accordingly, we may write the partially integrated Lin equation (3) as:

(7)   \begin{equation*}\frac{d}{dt}E_{\kappa}(t) = -\Pi(\kappa,t) - \int^{\kappa}_{0}dk\,D(k,t).\end{equation*}

Thus, the energy contained in modes 0\leq k \leq \kappa is lost partly to direct viscous dissipation and partly due to transfer to higher-wavenumber modes.This is the only concept of localness which is required for the Richardson-Kolmogorov picture in wavenumber space (K41).

This analysis holds for any wavenumber k=\kappa, but the most important case occurs at \kappa =k_{*}, which is the wavenumber where T(k,t) has its single zero-crossing. As is well known, the zeros of the transfer spectrum are given by:

(8)   \begin{equation*}T(0,t) =0;\qquad T(k_{*},t)=0; \quad \mbox{and} \quad \lim_{k \to \infty} T(k,t)=0: \end{equation*}

while, by simple calculus, the behaviour of the energy flux is given by:

(9)   \begin{equation*}\Pi(0,t) =0;\qquad \Pi(k_{*},t)=\Pi_{max}; \quad \mbox{and} \quad \lim_{k \to \infty} \Pi(k,t)=0.\end{equation*}

It follows from conservation of energy that the maximum value that \Pi_{max} can take is the rate of viscous dissipation, thus we have the general result:

(10)   \begin{equation*}\Pi_{max} \leq \varepsilon;\end{equation*}

where the equality applies if the local viscous dissipation can be neglected at k=k_{*}.

In our next post, we will take a more critical look at this criterion.

References.
[1] L. Onsager. The Distribution of Energy in Turbulence. Phys. Rev., 68:286, 1945.
[2] W. David McComb. Homogeneous, Isotropic Turbulence: Phenomenology, Renormalization and Statistical Closures. Oxford University Press, 2014.

An assessment of Onsager’s concept of scale invariance: 1 / David McComb on the Physics of Turbulence by blogadmin is licensed under a Creative Commons Attribution CC BY 3.0

2 Replies to “An assessment of Onsager’s concept of scale invariance: 1”

  1. A little late with the welcoming you back to blogging. As mentioned in a comment to a much earlier post, this blog has been a helpful reference; once finished with some atomic-scale hydrodynamic modeling (CDFT) , I hope to look into stochastic closures for the NSE.

    Reply

  2. Thanks Jonathan, I appreciate that. Also, many thanks for pointing out the typos in this post. They were due to a mismatch between Latex and Quick Latex, as used in WordPress.

    Reply

Leave a Reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed.