The non-Markovian nature of turbulence 4: the Edwards energy balance as a Master Equation.
In this post we will rely on the book [1] for background material and further details. We begin with the well-known Lin equation for the energy spectrum in freely decaying turbulence, thus:
(1) ![]()
where ![]() is the transfer spectum: see [1] for further details. This equation is the Fourier transform of the better known Karman-Howarth equation in real space. But, although the KHE is a local energy balance in the separation of measuring points
is the transfer spectum: see [1] for further details. This equation is the Fourier transform of the better known Karman-Howarth equation in real space. But, although the KHE is a local energy balance in the separation of measuring points ![]() , the Lin equation is not actually a local energy balance in wavenumber space since the transfer spectrum depends on an integral of the triple-moment over all wavenumbers. For explicit forms, see [1].
, the Lin equation is not actually a local energy balance in wavenumber space since the transfer spectrum depends on an integral of the triple-moment over all wavenumbers. For explicit forms, see [1].
The energy spectrum is defined in terms of the covariance in wavenumber space (or spectral density) by the well-known relation:
(2) ![]()
but in theory it is more usual to work in terms of the latter quantity, and accordingly we transform (1) into
(3) ![]()
.
The Edwards statistical closure for the transfer spectrum may be written as:
(4) ![]()
where ![]() and the inverse modal response time is given by:
and the inverse modal response time is given by:
(5) ![]()
This controls the loss of energy from mode ![]() , while the term giving the gain to mode
, while the term giving the gain to mode ![]() from all the other modes takes the form:
from all the other modes takes the form:
(6) ![]()
Then, the Edwards form for the transfer spectral density may be written as:
(7) ![]()
and from (3) the Edwards theory gives the Lin equation as:
(8) ![]()
Our next step is to compare this to the Master Equation and for simplicity we will consider a quantum system which can exist in any one of a large number of discrete states ![]() , where
, where ![]() is a positive integer. The relevant equation is the Fermi master equation (see Section 9.1.2 of the book [2]), which may be written as:
is a positive integer. The relevant equation is the Fermi master equation (see Section 9.1.2 of the book [2]), which may be written as:
(9) 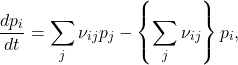
where: ![]() is the probability of the system being in state
is the probability of the system being in state ![]() ;
; ![]() is the conditional probability per unit time of the system jumping from state
is the conditional probability per unit time of the system jumping from state ![]() to state
to state ![]() ; and the principle of jump rate symmetry gives us
; and the principle of jump rate symmetry gives us ![]() .
.
Either from this comparison with the Fermi master equation or from comparison with other master equations such as the Boltzmann equation, it is clear that the Edwards theory of turbulence is a Markovian approximation to turbulence which is itself non-Markovian. The two questions which now arise are: first, what are the implications for the other closures due to Kraichnan and to Herring? And, secondly, how did the Markovian nature of the Edwards theory come about? These will be dealt with in the next two posts?
[1] W. David McComb. Homogeneous, Isotropic Turbulence: Phenomenology, Renormalization and Statistical Closures. Oxford University Press, 2014.
[2] W. David McComb. Study Notes for Statistical Physics: A concise, unified overview of the subject. Bookboon, 2014. (Free to download from Bookboon.com)



