Superstitions in turbulence theory 1: the infinite Re limit of the Navier-Stokes equation is the Euler equation!
I recently posted blogs about the Onsager conjecture [1]; the need to take limits properly (Onsager didn’t!); and the programme at MSRI Berkeley, which referred to the Euler equation as the infinite Reynolds number limit, in a series of posts from 5 – 19 August just past. A later notification about the MSRI programme no longer made that claim; and I speculated (conjectured?) that this might not be unconnected from the appearance of the paper [2] on the arXiv! Now the Isaac Newton Institute is having a new programme on mathematical aspects of turbulence over the first half of next year, and their theme dwells on how the mathematics underlying ‘the proof of the Onsager conjecture … can bring insights into the dissipative anomaly conjecture, a.k.a. Kolmogorov’s zeroth law of turbulence’.
The idea of a dissipation (or dissipative) anomaly goes back to Onsager’s conjecture [1] made in 1949 when turbulence studies were still in their infancy. Although the alternative expression (i.e Kolmogorov’s zeroth law) has also been used, I have no idea who formulated it; nor of the reasoning that lies behind it. While Kolmogorov may have formulated laws in statistics (I am indebted to Mr Google for this information!), his contributions to turbulence do not qualify for the description ‘physical laws’. However, an irony about the way in which Onsager came to his conclusion about a dissipative anomaly recently dawned on me, and the point of this post is to share that with you.
Onsager’s starting point was Taylor’s (1935) expression for the turbulent dissipation [3] thus:
(1) 
where 
is the dissipation rate, 
is the root mean square velocity, 
is the integral scale, and 
is a coefficient which may depend on the Reynolds number 
, which is formed from the integral scale and the rms velocity. In 1953, Batchelor [4] presented some results that suggested tended to a constant with increasing Reynolds number.. Nevertheless, this expression was the subject of some debate over the years (although its equivalent for shear flows was widely used in both research and practical applications), until Sreenivasan’s survey papers on grid turbulence [5] in 1984 and on direct numerical simulations [6] in 1998 established the characteristic asymptotic shape of this curve. This work had a seminal effect on the subject and a general account of work in this area can be found in the book [7].
However, it was suggested by McComb et al in 2010 [8] that the Taylor’s expression for the dissipation (1) is actually a surrogate for the peak inertial flux 
. See the figure below, which is taken from that paper. It shows from DNS that the group 
behaves like for all Reynolds numbers, whereas the behaviour of the dissipation is quite different at low Reynolds numbers.
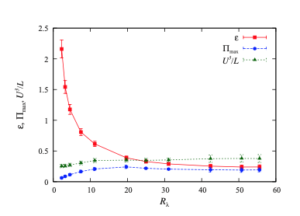
as 
corresponding to the onset of the Kolmogorov 
law.
In other words, when Onsager deduced from Taylor’s expression that the dissipation did not depend on the viscosity, he was actually deducing that the peak inertial flux did not depend on the viscosity. And indeed it doesn’t!
[1] L. Onsager. Statistical Hydrodynamics. Nuovo Cim. Suppl., 6:279, 1949.
[2] W. D. McComb and S. R. Yoffe. The infinite Reynolds number limit and the quasi-dissipative anomaly. arXiv:2012.05614v2[physics.flu-dyn], 2021. 28.
(N.B. This paper is presently under revision and will be posted again, possibly with a change of title.)
[3] G. I. Taylor. Statistical theory of turbulence. Proc. R. Soc., London, Ser. A, 151:421, 1935.
[4] G. K. Batchelor. The theory of homogeneous turbulence. Cambridge University Press, Cambridge, 1st edition, 1953.
[5] K. R. Sreenivasan. On the scaling of the turbulence dissipation rate. Phys. Fluids, 27:1048, 1984.
[6] K. R. Sreenivasan. An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids, 10:528, 1998.
[7] W. David McComb. Homogeneous, Isotropic Turbulence: Phenomenology, Renormalization and Statistical Closures. Oxford University Press, 2014.
[8] W. David McComb, Arjun Berera, Matthew Salewski, and Sam R. Yoffe. Taylor’s (1935) dissipation surrogate reinterpreted. Phys. Fluids, 22:61704, 2010.
[9] W. D. McComb, A. Berera, S. R. Yoffe, and M. F. Linkmann. Energy transfer and dissipation in forced isotropic turbulence. Phys. Rev. E, 91:043013, 2015.
