In a previous blog post, we analysed Pool Splitting Behaviour and Equilibrium Properties in Cardano’s Rewards Scheme, demonstrating results from experiments that were carried out using a simulation engine that we developed. This time, we are here to explain in detail how this tool works and go over the design choices and assumptions that were made while modelling the pooling process of Cardano. We also make the code available on Github for others to inspect as well as extend it to perform additional experiments and capture a more diverse set of behaviours.
Simulation Flow
At the start of a simulation run, each agent is allocated some stake and a cost value that will be incurred should they decide to run a pool, and the system starts off without any pools. In each round, all agents take turns in random order, form a potential delegation and pool operation strategy and adopt the one that yields the highest expected utility for them. However, if the utility they receive from their established strategy—augmented by a small amount to account for inertial forces—is higher than the expected utilities of the new strategies, then they do not make any changes. If the simulation reaches a point where no agent deviates from their chosen strategy for a number of rounds, then an equilibrium is declared, and the simulation terminates. If no equilibrium is reached, then the simulation terminates after a pre-defined number of maximum iterations is exceeded.
Behaviour Modelling
To make the simulation steps meaningful, we had to model the way stakeholders make different decisions along the way. How does an agent decide whether to operate a pool or delegate their stake to the pools of others, i.e. how do they assign value to each potential strategy? If they choose to become operators, how do they select their pledge and profit margin? And if they choose to become delegators, how do they decide which pool(s) to allocate their stake to? We will go through our reasoning in the following paragraphs.
Forming a delegation strategy. The simplest question to address—at least in a theoretical setting—is that of delegation, i.e., given a set of active pools, each with a certain pledge, margin, cost and total stake, where should one delegate their stake to, with the goal of maximising their profit. This is where the metric of desirability comes in handy, which represents the share of a pool’s expected profits that is allocated to the pool’s delegators proportionally to their delegated stake. Armed with this metric, the agents rank all pools of the system and choose to delegate their stake to the one(s) with the highest desirability—prioritising those that are not yet saturated—as they expect to gain higher rewards per unit of stake from them. Note that this reflects non-myopic thinking on behalf of the agent; we do also model myopic thinking – see paragraph “Stakeholder profiles” below.
Forming a pool operation strategy. Things get a bit more complicated when it comes to making decisions about potential pools to operate. Since our simulation supports multi-pool strategies, a prospective pool operator first needs to decide how many pools to run and then also choose suitable values for the pledge and profit margin of each pool. To find a promising solution, we employ a local search similar to hill climbing, which transpires as follows for an agent with stake 𝑠:

To clarify the margin calculation process (step 4 above), the agent ranks all pools that belong to other agents based on their desirability and attempts to surpass the desirability of the k-ranked pool with their first pool, the desirability of the (k-1)-ranked pool with their second pool, and so on, up to pool t which attempts to beat the desirability of the (k+1-t)-ranked pool. Since they attempt to replace different pools from the top 𝑘, different pools of the same agent may end up with distinct margin values.
Economies of scale. The cost value that each agent is assigned at the start of the simulation corresponds to the cost they bear when operating a single pool. Since our simulation supports multi-pool strategies, we had to model the impact that economies of scale hav
e, namely that operating multiple pools effectively reduces the average cost the agent incurs per pool. We employ a simple model, which dictates that every additional pool of an agent costs a fraction φ of their original cost. Therefore, an agent with an initial cost value of c who operates t pools calculates their average cost per pool as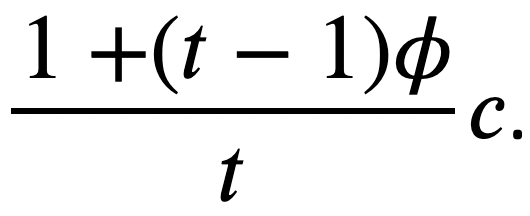
Utility calculations. In our context, the utility of an agent is equivalent to the profit they (expect to) make through staking. For delegators, this is strictly a non-negative value, but operators—who incur expenses—may also sustain losses, should their pools not be successful in attracting delegations. Following the approach of the academic paper that introduced Cardano’s reward sharing scheme, we grant our agents a degree of far-sightedness when it comes to the calculation of pool rewards, i.e., the default behaviour of the agents is to calculate the non-myopic utility of a strategy. Specifically, agents assume that a pool will become saturated if it belongs in the top-k desirable pools and that otherwise it will end up only with the owner’s stake, so they use this non-myopic stake to calculate the rewards that a pool will receive and their share of it.
Stakeholder profiles. To make the simulation engine easier to extend, we describe the behaviour of the agents through profiles. In the paragraphs above, we described the default behaviour of our agents, which corresponds to the non-myopic stakeholder profile, but we have also implemented a profile for myopic behaviour and a profile for abstention. The myopic stakeholder mainly differs from the non-myopic one in the way they calculate their expected utility, as they use the current stake of a pool (instead of the non-myopic one) when calculating its rewards. Accordingly, when ranking the pools of the system based on their desirability (e.g., when deciding where to delegate their stake or when calculating a suitable margin for their pool), a myopic stakeholder will consider how desirable a pool is based on its current stake. The abstainer, on the other hand, is a profile for stakeholders that do not engage with the protocol at any point, i.e., they do not own pools nor delegate their stake to the pools of others. Additional profiles can be created to add alternative behaviours or assumptions, e.g., on how economies of scale are modelled or how agents distribute their stake as pledge across their pools. During a particular simulation run, agents of multiple different profiles can be included by specifying a percentage for each profile.
Source Code
The simulation engine is written in Python 3.9 and its source is available on GitHub under the Apache-2.0 License. Everyone is welcome to review it, report potential issues, propose changes, or contribute to it in any other way they see fit by creating a pull request. In particular, we encourage people to run their own experiments and share the results and their thoughts about them with the community. In the following paragraph, we briefly go through different ways to configure and run the simulation, and we provide some examples as starting points.
Configurability & Examples
The simulation engine has been designed to be highly configurable, in order to accommodate a variety of experiments. Upon issuing the execution command for a simulation, the user can determine the number of agents and their characteristics (stake, cost and behavioural profile distribution), the values for the variables of the reward sharing scheme (target number of pools k, stake influence factor a0), the order with which agents make their moves during each round, the metrics to track during the simulation (e.g., pool count, total pledge, Nakamoto coefficient), and more. An interesting element that is also configurable is the reward function that is used in the simulation, i.e., the function that determines how many rewards a pool will receive depending on its characteristics. We have already added some options other than the original reward function that is currently used in Cardano (e.g., the one that was proposed in CIP-7), and it is very easy to add more, as long as they are similar to that one (reward functions that are very different may require further changes in our modelling process).
Note that there are default values in place for all the parameters, so it is also possible to run a simulation without specifying any of the above. A file named args.json is created upon execution of the simulation, which lists all parameter values that were used (it is also possible to provide an args.json file to read all the argument values from, but this is not the default behaviour).
To run an experiment with the default configuration, one can open a terminal in the root directory of the project and run the following command (assuming that the python command corresponds to a Python 3.9 installation):
python main.py
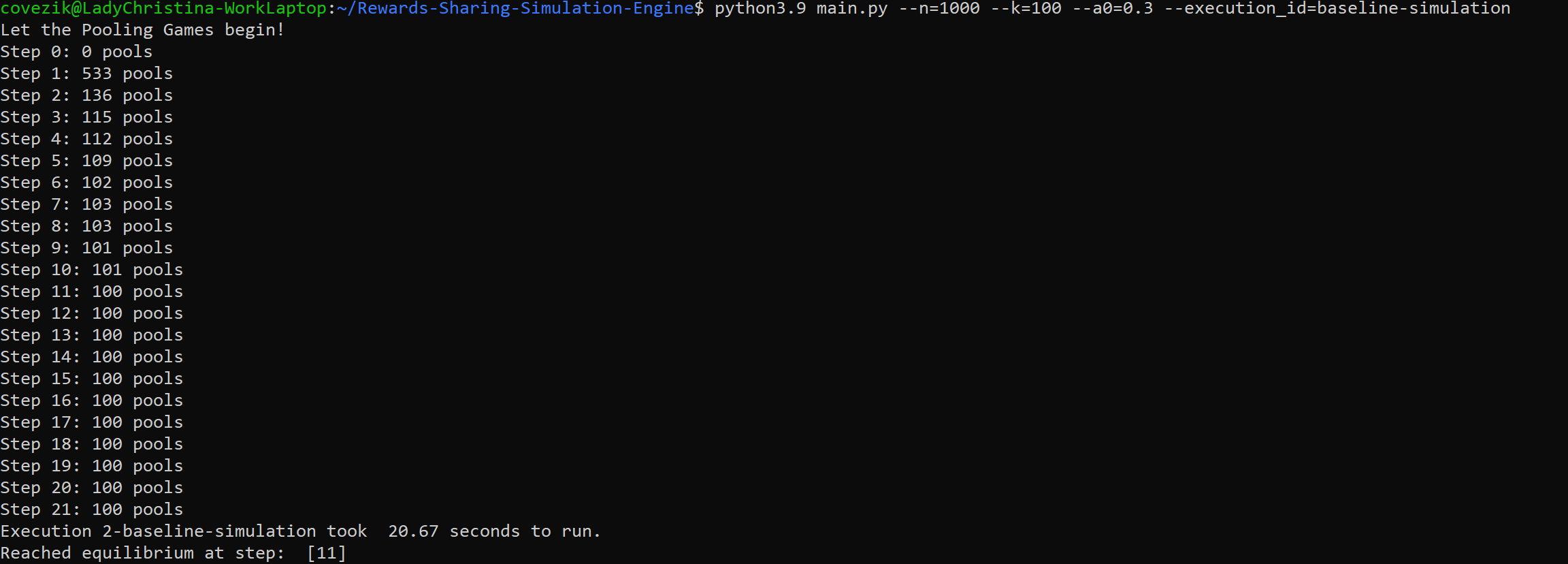
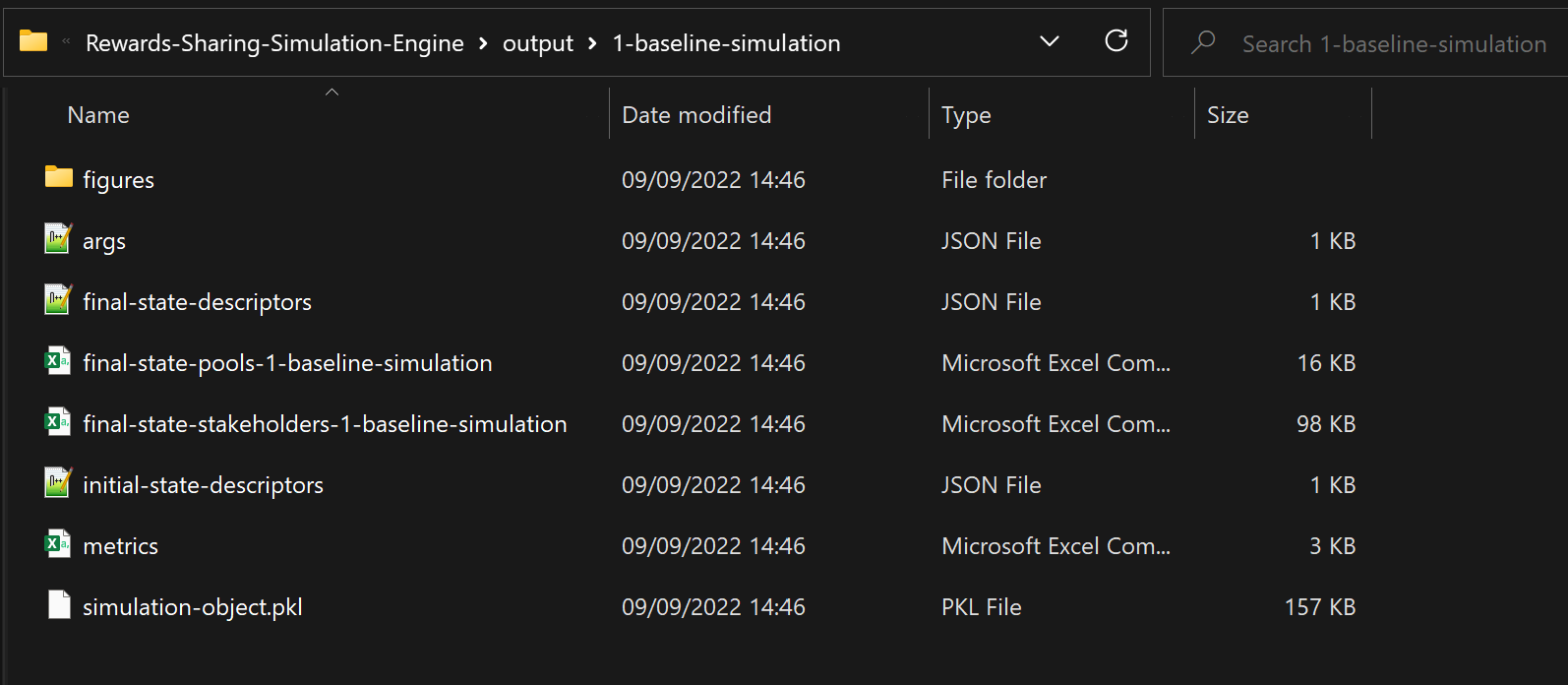
A message is displayed at the terminal at every step of the process (see Figure 1), and, upon termination of the simulation, some relevant files are produced and saved under the “output” directory, which is created if it does not already exist (see Figure 2). An execution id can also be associated with a simulation, so that its output is named accordingly. If no identifier is provided, then one is generated based on the values of the parameters that were used.
Alternatively, the user can provide specific values for some arguments, like this:
python main.py --n=1000 --k=150
To make the results easy to reproduce, the user can provide a number that serves as the seed for any pseudorandom processes used in the simulation (e.g. the “random” order that the agents get activated in):
python main.py --seed=42 --execution_id=simulation-with-seed-42
There is also the option to run multiple simulations with different configurations at once, using multiprocessing. To do that, we can run another script, named batch-run.py. Running it with the default configuration produces 5 instances of the simulation, differing only in the value of the target number of pools k, but it is also possible to get simulations with different number of agents, different a0 values, and more. The following example triggers the execution of 10 simulations, all of which have 1000 stakeholders and a0 = 1, but different values for k (50, 100, …, 450, 500).
python batch-run.py --n=1000 --alpha=1 --k 50 501 50 --execution_id=batch-run-n-1000-alpha-1-k-50-500
To run multiple experiments, one can also write a script that issues any combination of the above commands. In the Github repository, we have included a file with the experiments described in the documentation Examples page.
For more information and examples on the different ways to execute simulations, one can see the relevant Github page and the supporting documentation. Specifically, in the documentation, we present all arguments that the simulation accepts and their default values, we explain what each output file is about, and we provide more examples for running simulations in various ways.
Limitations & Future Directions
The simulation engine we developed offers some basic functionalities for modelling the pooling process of Cardano, and, as we saw above, can be configured to represent different stakeholder populations, track different metrics, and more. Nonetheless, there are several ways with which it can be improved or extended to offer more functionality or come closer to the real-life deployment of Cardano. Some options we have considered are the following:
- Include different profiles of stakeholders, e.g., a profile that only adopts delegation strategies to represent people who lack the technical knowledge or time to become operators (can also be modelled by agents with very high cost using our current simulation, but it would be more efficient to use profiles) or a profile that has a different goal other than maximizing their utility (e.g., subverting the system).
- Associate a “reputation” with each pool operator, which is taken into consideration by the stakeholders when deciding on a delegation strategy. This reputation can either be static or change dynamically based on the actions of the agents (e.g., reputation is increased if an agent keeps their pool open for more than x rounds or reputation is decreased if an agent engages in pool-splitting behaviour).
- Integrate an exchange rate in the simulation to examine the effects of a volatile market / market shock. Since the costs that operators incur are in a different currency (fiat) than the one they receive their rewards in (Ada), it would be interesting to have a dynamic exchange rate between the two in the simulation.
- Adapt the simulation to different reward schemes / blockchains. The simulation engine already supports different functions for calculating the rewards of a pool, but with the assumption that they are similar to the one currently used in Cardano (e.g., that there is a saturation point for each pool at which maximal rewards are earned); it would be interesting to generalise the code to other cases too, and effectively compare the reward sharing scheme of Cardano with those of other blockchains.
Another useful direction is to improve the code of the simulation in terms of performance, maintainability or user-friendliness. Anyone interested is welcome to contribute to our repository, either drawing inspiration from the above or exploring their own ideas.
Key takeaways
- We have developed a simulation engine that models the pooling process of Cardano and supports multi-pool strategies.
- The simulation is highly configurable; both its input and its output can change to match a user’s needs in several ways.
- The source code and the documentation of the simulation are publicly available. There are many improvements or extensions that can be made – contributions are welcome!
by Christina Ovezik & Aggelos Kiayias Posted 9 Sept, 2022




Thanks for sharing the post.
Thank you for sharing the data,
Thank you for this marvellous work!
Have any simulations been run that have “fixed cost” component i.e. amount of Ada a pool operator receives from the epoch reward pot for the pool, before they receive the configured margin %?