The Edinburgh Analysis Seminar is held in person at 3.05pm on Mondays in JCMB. It is currently organised by Linhan Li and Leonardo Tolomeo

Monday, 5 May 2025

JCMB 6206

Regularity for semilinear variational problems with a topological constraint

Anna Skorobogatova (ETH Zürich)

Abstract:

I will discuss the regularity of solutions to a class of semilinear free boundary problems in which admissible functions have a topological constraint, or spanning condition, on their 1-level set. This constraint forces the 1-level set, which is a free boundary, to behave like a surface with singularities, attached to a fixed boundary frame, in the spirit of the set-theoretic Plateau problem. Two such free boundary problems that have been well-studied are the minimization of capacity among surfaces sharing a common boundary and an Allen-Cahn approximation of the set-theoretic Plateau problem. We establish optimal Lipschitz regularity for solutions, and analytic regularity for the free boundaries away from a codimension two singular set. We further characterize the singularity models for these problems as conical critical points of the minimal capacity problem, which are closely related to spectral optimal partition and segregation problems. This is joint work with Mike Novack and Daniel Restrepo.

Spring 2025

Monday, 5 May 2025

JCMB 6206

Regularity for semilinear variational problems with a topological constraint

Anna Skorobogatova (ETH Zürich)

Abstract:

Monday, 31 March 2025

JCMB 6201

Sharp spectral projection estimates for the torus

Daniel Pezzi (Johns Hopkins)

Abstract:

It is a natural, but oftentimes difficult, question to deduce information about a periodic function from its Fourier series expansion. Spectral projection estimates are one way to explore this connection. If a function has its spectrum contained in an annulus, how large can the function be in an L^p norm? For unit width annuli this question is answered by the universal estimates of Sogge. If the projection operator projects onto an eigenspace, this is the Discrete Restriction conjecture of Bourgain. We present sharp estimates for intermediate cases for a large subset of the relevant parameters, which addresses a conjecture of Germain and Myerson. We will discuss the techniques used, similarities and differences to the case of general manifolds, and potential future avenues of attack.

Wednesday, 26 March 2025

Usha Kasera Lecture Theatre (Old College)

Maxwell Analysis Mini-symposium

1:00pm Pierre Germain (Imperial College)

Asymptotic stability of solitary waves in nonlinear dispersive equations

I will present some recent developments on the asymptotic stability of solitary waves in nonlinear dispersive equations, focusing on the 1D case, in particular nonlinear Klein-Gordon and nonlinear Schrodinger equations. New ideas involving the distorted Fourier transform and nonlinear resonances have led to important progress. I will rely on joint work with Fabio Pusateri and Charles Collot.

2:30pm Laure Saint-Raymond (IHES)

The effect of viscosity on internal waves

In presence of topography, forcing 2D inviscid internal waves leads to the formation of singular geometric patterns, called “attractors”,
which accumulate most of the energy. Our goal is to understand how this phenomenlogy is modified by a small viscosity.

Monday, 17 March 2025

JCMB 6206

Pathwise local well-posedness of stochastic nonlinear wave equations with multiplicative noises

Jiawei Li (University of Edinburgh)

Over the last decade, there has been a significant development in the study of stochastic dispersive PDEs, broadly interpreted with random initial data and/or additive stochastic forcing, where the difficulty comes from roughness in spatial regularity. In this talk, we consider the well-posedness of stochastic nonlinear wave equations with multiplicative noises, whose Itô solutions were constructed in 80s. Results on pathwise well-posedness for stochastic nonlinear wave equations (SNLW) will be presented. The main challenge of this problem comes from the deficiency of temporal regularity. We overcome this issue by bridging the theory of controlled rough paths and the Fourier restriction norm method.

Monday, 10 March 2025

JCMB 6206

A problem in quasilinear wave equations

Pieter Blue & Jan Sbierski (University of Edinburgh)

Abstract:

A major open problem in the study of the incompressible Euler equations is to understand stable shock formation in 3 dimensions and the global dynamics of such solutions. Recent work by Christodoulou has made substantial progress for irrotational fluid flow, in which case the equations reduce to a system of quasilinear wave equations. Major themes in this work are weak and classical solutions, globally hyperbolic developments, uniqueness, shock formation, and shock development. We will present recent work on uniqueness aspects for quasilinear wave equations and give an example of a quasilinear wave equation for which all the aspects of Christodoulou’s approach to shocks can be proven globally.

This talk is based on collaborative work with Eperon, Reall, Abbrescia, and Speck.

Monday, 3 March 2025

JCMB Lecture Theatre C

Convex sets can have interior hot spots

Juame de Dios Pont (ETH Zürich)

Abstract:

A homogeneous, insulated object with a non-uniform initial temperature will eventually reach thermal equilibrium. The Hot Spots conjecture addresses which point in the object takes the longest to reach this equilibrium: Where is the maximum temperature attained as time progresses?
Rauch initially conjectured that points attaining the maximum temperature would approach the boundary for larger times. Burdzy and Werner disproved the conjecture for planar domains with holes. Kawohl, and later Bañuelos-Burdzy, conjectured that the conjecture should still hold for convex sets of all dimensions.

Wednesday, 26 February 2025

Elizabeth Templeton Lecture Room, New College, Mound Pl

LMS Harmonic Analysis & PDE network meeting

Sam Chow (University of Warwick)
Nicola Visciglia (Università di Pisa)
Runlian Xia (University of Glasgow)
Jim Wright (University of Edinburgh)

Monday, 10 February 2025

JCMB 6206

Three discrete maximal functions in high dimensions – Gaussians, balls and spheres

Błażej Wróbel (University of Wrocław)

Abstract:

High-dimensional phenomena constitute a research theme that has been present in harmonic analysis for several decades. It was initiated by E. M. Stein in 1980s and important contributions were made by J. Bourgain, A. Carbery and D. Müller. The study of dimension-free estimates for Hardy-Littlewood maximal functions in the discrete setting was initiated several years ago by J. Bourgain, E. M. Stein, M. Mirek and myself. One of the most important open problems in this field is a question of E. M. Stein about a dimension-free estimates for discrete maximal function over balls.

I will discuss three discrete maximal functions: for Gaussians, balls, and spheres. The study of dimension-free estimates for these maximal functions requires bounding certain multiplier symbols, which are highly symmetric exponential sums. This calls for interdisciplinary tools from analytic number theory (Waring’s problem) and combinatorics. A preliminary step in the case of balls and spheres is a count of lattice points in these sets which has to be performed in a uniform (dimension-free) manner. I will report on recent progress with M. Mirek and T.Z. Szarek (spheres and Gaussians), and with J. Niksiński (balls and spheres). In particular, I will present an affirmative answer to Stein’s question when the supremum is restricted to small enough radii.

Monday, 3 February 2025

JCMB 6206

Hyperbolic nonlinear Schrödinger equations

Yuzhao Wang (University of Birmingham)

Abstract:

Hyperbolic Schrödinger equations have attracted increasing attention in recent years due to their newly discovered connections with water waves and the Boltzmann equation. In this talk, we begin by exploring some of these connections. We then present some recent advances in the solution theory of hyperbolic nonlinear Schrödinger equations on partial periodic and periodic domains. Specifically, we will discuss Strichartz estimates, which relate to the l^2 decoupling theory of non-positive Gaussian curvature surfaces, and unconditional well-posedness, which reduces to lattice counting estimates by using infinite iterations of normal form reduction.

Monday, 27 January 2025

JCMB 6206

Regularity of maximal functions

Julian Weigt (University of Warwick)

Abstract:

The classical Hardy-Littlewood maximal function theorem states that the Hardy-Littlewood maximal operator is a bounded operator on L^p(ℝ^d) if and only if 1 < p <= ∞. In 1997 Juha Kinnunen proved the corresponding result for the gradient of the maximal function, i.e. that the L^p(ℝ^d)-norm of the gradient of the maximal function is controlled by the L^p(ℝ^d)-norm of the gradient of the function if 1 < p <= ∞. However, he provides no counterexample in the endpoint, leaving open the possibility that the gradient bound in fact holds also for p = 1.

In 2004 Hajłasz and Onninen formally posed the question if the Hardy-Littlewood maximal operator on ℝ^d satisfies the endpoint gradient bound. It has since attracted considerable attention, motivated by to the elementary nature of the maximal operator and by the relative simplicity of the proof of the Hardy-Littlewood maximal function theorem and of Kinnunens 1997 result. Many special cases, generalizations and variations of this problem have been explored, with partial success. The original question by Hajłasz and Onninen remains unanswered.

Monday, 20 January 2025

JCMB 6206

Symmetric low-regularity integrators for dispersive nonlinear equations

Georg Maierhofer (University of Cambridge)

Abstract:

Dispersive nonlinear partial differential equations can be used to describe a range of physical systems, from water waves to spin states in ferromagnetism. The numerical approximation of solutions with limited differentiability (low-regularity) is crucial for simulating fascinating phenomena arising in these systems including emerging structures in random wave fields and dynamics of domain wall states, but it poses a significant challenge to classical algorithms. Recent years have seen the development of tailored low-regularity integrators to address this challenge. Inherited from their description of physicals systems many such dispersive nonlinear equations possess a rich geometric structure, such as a Hamiltonian formulation and conservation laws. To ensure that numerical schemes lead to meaningful results, it is vital to preserve this structure in numerical approximations. This, however, results in an interesting dichotomy: the rich theory of existent structure-preserving algorithms is typically limited to classical integrators that cannot reliably treat low-regularity phenomena, while most prior designs of low-regularity integrators break geometric structure in the equation. In this talk, we will outline recent advances incorporating structure-preserving properties into low-regularity integrators. Starting from simple discussions on the nonlinear Schrödinger and the Korteweg–de Vries equation we will discuss the construction of such schemes for a general class of dispersive equations before demonstrating an application to the simulation of low-regularity vortex filaments. This is joint work with Yvonne Alama Bronsard, Valeria Banica, Yvain Bruned, Yue Feng, Chushan Wang and Katharina Schratz.

Monday, 13 January 2025

JCMB 5327

On some Thomas-Fermi type variational problems

Damiano Greco (University of Edinburgh)

Abstract:

We consider two different Thomas–Fermi type problems, a repulsive and an attractive case.

The first problem concerns studying the existence and qualitative properties of the minimizers for a Thomas—Fermi type energy functional with non local repulsion involving a convolution with the Riesz kernel and an interaction with an external potential. Under mild assumptions on the latter, we can establish uniqueness and qualitative properties such as positivity, regularity, and decay at infinity of the global minimizer.

The second problem concerns the study of optimizers of the Gagliardo–Nirenberg type inequality again involving a convolution with the Riesz kernel. Such a problem is well understood in connection with Keller—Segel models and appears in the study of Thomas—Fermi limit regimes for the Choquard equations with local repulsion and non local attraction.

Autumn 2024

Maxwell Analysis Mini-Symposium

The slides of the talks can be found on Heriot-Watt Analysis seminar webpage.

27 November 1:30 PM to 5:00 PM,

Sydney Smith Lecture Theatre at the Medical School.

1:30pm François Genoud: Finite time blow-up for the critical nonlinear Schrödinger equation on a star graph

2:30pm Kaj Nyström: Caloric Measure and Parabolic Uniform Rectifiability

3:30pm Coffee Break

4:00pm Máté Weirdl: Basecamp for convergence of ergodic averages along subsequences

——–

Title: Finite time blow-up for the critical nonlinear Schrödinger equation on a star graph

François Genoud (EPFL)

Abstract:
The talk will start with a brief history of finite time blow-up solutions for critical nonlinear Schrödinger equations (NLS) in various contexts. Once the stage is set, the construction of a finite time blow-up solution for the critical NLS on a star graph with delta interaction will be presented. The simplest configuration of a graph with two branches corresponds to the NLS on the line with a “delta potential” at the origin. The general case involves a one-dimensional Laplace operator on the graph with Robin boundary conditions at the vertex. The blow-up analysis relies on the resolution of the nonlinear Cauchy problem within the domain of the corresponding linear operator. This is joint work with Stefan Le Coz and Julien Royer.

—-

Title: Caloric Measure and Parabolic Uniform Rectifiability

Kaj Nyström (Uppsala University)

Abstract:

The heat equation stands as a cornerstone in mathematics, physics, and various applied fields, describing the distribution of heat (or diffusion of particles) over time. A fundamental question associated with this equation is the Dirichlet problem, which seeks solutions given boundary conditions—a challenge that links the behavior of the heat equation to the geometry of underlying spaces. In recent collaborative work with S.~Bortz, S.~Hofmann, and J-M.~Martell, we address two longstanding conjectures on the $L^p$ Dirichlet problem for the heat equation, caloric measure, and parabolic uniform rectifiability. First, we establish that, for parabolic Lipschitz graphs, the solvability of the $L^p$ Dirichlet problem is equivalent to parabolic uniform rectifiability. Second, we show that, in the broader setting of parabolic Ahlfors-David regular boundaries, the solvability of the $L^p$ Dirichlet problem necessitates parabolic uniform rectifiability. This talk will outline these results, highlighting the intricate interplay between the heat equation and geometric regularity.

—–

Title: Basecamp for convergence of ergodic averages along subsequences

Máté Weirdl (The University of Memphis)

Abstract: The purpose of this talk is to give a summary of the ergodic theoretical background for subsequence ergodic theorems (pioneered by von Neumann, Bellow,

Krengel, Bourgain): why we want to extend the ergodic theorem to subsequences in the first place; periodic and aperiodic systems; mean ergodic theorem; baby spectral theorem; good and bad sequences; pointwise ergodic theorem as a consequence of the Hardy-Littlewood maximal inequality; transference principle of A. Calderón.

The audience is assumed to have a background in real analysis, including Hilbert spaces, but not in ergodic theory.

Monday, 16 September 2024

JCMB 6206

The dimension of random subsets of Cantor sets defined by trees of coin flips

Lauritz Streck (University of Edinburgh)

Abstract: Allaart and Jones considered a procedure to choose random subsets of a Cantor set with a binary tree of coin flips and proved upper and lower bounds for the dimension of these sets. In the talk, we show the exact value of this dimension. While the problem is phrased in terms of fractal sets, the proof relies only on counting and energy arguments.

Monday, 23 September 2024

JCMB 6206

Pointwise localization and sharp weighted bounds for Rubio de Francia square functions

Mikel Florez (BCAM)

Abstract:

In this talk, we will show a new pointwise sparse bound for the Rubio de Francia square functions. These sparse bounds lead to quantified weighted inequalities. We will also present that the L^2 conjecture holds for radially decreasing even weights and in full generality for the Walsh group analogue.

Recall that the Rubio de Francia square function is the square function formed by frequency projections over a collection of disjoint intervals of the real line. In the first part of the talk, we will give the background of the problem. In the second part, we will explain the new results mentioned above.

This talk is based on a joint work with F. Di Plinio, I. Parissis and L. Roncal.

Monday, 30 September 2024

JCMB 5328

Dimension interpolation and exceptional set estimates

Ana Emilia de Orellana (St. Andrews)

Abstract: Since Marstrand’s work on orthogonal projections, exceptional set estimates for such projections have been widely studied. Salem sets, i.e. sets for which the Fourier and Hausdorff dimension coincide, have no such exceptions, but using the Fourier dimension alone to improve exceptional set estimates leads to discontinuous bounds. In this talk we will see what conditions we need on the Fourier decay of measures to ensure continuity of the bounds. Joint work with Jonathan Fraser.

Monday, 7 October 2024

JCMB 6206

Fourier multipliers on SL(2,Z) and SL(2,R)

Runlian Xia (University of Glasgow)

Abstract:

The Hilbert transform $H$ is a basic example of Fourier multipliers. Its behaviour on Fourier series is the following:

$</div> <div>\sum_{n\in \mathbb{Z}}a_n e^{inx} \longmapsto \sum_{n\in \mathbb{Z}}m(n)a_n e^{inx},</div> <div>$

with $m(n)=-i\,{\rm sgn} (n)$ . Riesz and Cotlar proved that $H$ is a bounded operator on $L_p(\mathbb{T})$ for all $1<p<\infty$ . In this talk, we will first introduce a generalised Cotlar identity and a geometric form of

Hilbert transforms for groups acting on $\mathbb{R}$ -trees, then we will focus on the case of $\SL (2,\Z)$ which is a lattice of $\SL (2,\R)$ . The final goal is to discuss how Hilbert transforms on $\SL (2,\Z)$ can be extended to an $L_p$ -bounded Fourier multiplier on $\SL (2,\R)$ using a transference method.

Based on a joint work with A. Gonz\’alez-P\’erez and J. Parcet, and an ongoing project with Simeng Wang and Gan Yao.

see PDF

Monday, 14 October 2024

JCMB 5328

Sharp Fourier restriction over finite fields

Cristian González-Riquelme (Instituto Superior Tecnico in Lisbon)

Abstract:

Sharp Fourier restriction theory has been a topic of interest over the last decades. On the other hand, efforts have been made in order to develop the theory of Fourier restriction over finite fields.

In this talk, we will present some recently made developments (in a joint work with Diogo Oliveira e Silva) in the intersection of these two topics.

Monday, 21 October 2024

JCMB 6206

Uniform Boundedness for Linearised Gravity on Schwarzschild from the Canonical Energy

Sam Collingbourne (University of Edinburgh)

Abstract: In this talk, I will discuss a robust method for producing a conservation law for linearised gravity on a stationary spacetime: the canonical energy of Hollands and Wald. Whilst its coercivity properties are obscure, I will argue that it can be used to obtain a uniform boundedness result for the gauge invariant Teukolsky variables, on the 4-dimensional Schwarzschild spacetime, which govern the linearised dynamics. Remarkably, this does not rely on the (decoupled) Teukolsky equation or the transformation theory associated to it. Time permitting, I will discuss recent progress towards producing a coercive estimate for linearised gravity on the higher dimensional Schwarzschild solution where both the decoupling and transformation theory fails. This work is joint with Gustav Holzegel.

Scottish-Basque Analysis meeting

Room 2.30, Edinburgh Futures Institute, 1 Lauriston Place, October 28-30, 2024

https://www.icms.org.uk/workshops/2024/scottish-basque-meeting-analysis

Monday, 4 November 2024

Theatre 201, Geology/Grant Institute

An intersection of CS and harmonic analysis: approximating matrix p to q norms

Dominique Maldague (University of Cambridge)

Abstract: In Fourier restriction theory, we bound exponential sums whose frequencies lie in sets with special properties, e.g. random sets or curved sets. Bourgain, Demeter, and Guth proved sharp decoupling inequalities, which show that many such functions enjoy square root cancellation behavior. This theory lies in the larger context of bounding matrix p to q norms, which is well-studied in the CS literature. We will discuss a new polynomial time algorithm of myself, Guth, and Urschel that is inspired by Fourier restriction theory and which reduces the multiplicative error of computing matrix 2 to q norms from roughly n^{1/q} to n^{1/2q}, where n is the size of the matrix.

Monday, 11 November 2024

JCMB 5328

Counting Rational Points near Smooth Manifolds

Rajula Srivastava (University of Bonn and the Max Planck Institute for Mathematics)

Abstract:

How many rational points with denominator of a given size lie within a certain distance from a compact, ”non-degenerate” manifold? This talk is about some recent progress towards answering this question. We shall describe how the geometric and analytic properties of the manifold play a key role in determining this count, and present a heuristic for the same. We shall then discuss how Fourier analytic techniques can be exploited to establish the desired asymptotic for rational points near manifolds satisfying certain strong geometric conditions. The key proof ingredient is a bootstrapping argument relying on Poisson summation, projective duality and oscillatory integral techniques.

Monday, 18 November 2024

JCMB 6206

Stability and instability of extremal black holes

Dejan Gajic (Leipzig University)

Abstract: Extremal black holes are critical members of families of black hole spacetime solutions to Einstein’s equations of general relativity that lie exactly on a phase transition from “black hole” to “no black hole”. As a result, they exhibit several interesting dynamical phenomena that are not present in sub-extremal (“sub-critical”) black holes. Most notably, the question of their dynamical stability under small initial data perturbations remains open. I will formulate what “stability” of extremal black hole might mean and then discuss why a positive answer to the stability question is much more subtle than in the sub-extremal setting by considering a simplified problem, the linear wave equation on an fixed extremal Kerr background spacetime.

Maxwell Analysis Mini-Symposium

The slides of the talks can be found on Heriot-Watt Analysis seminar webpage.

27 November 1:30 PM to 5:00 PM,

Sydney Smith Lecture Theatre at the Medical School.

1:30pm François Genoud: Finite time blow-up for the critical nonlinear Schrödinger equation on a star graph

2:30pm Kaj Nyström: Caloric Measure and Parabolic Uniform Rectifiability

3:30pm Coffee Break

4:00pm Máté Weirdl: Basecamp for convergence of ergodic averages along subsequences

——–

Title: Finite time blow-up for the critical nonlinear Schrödinger equation on a star graph

François Genoud (EPFL)

—-

Title: Caloric Measure and Parabolic Uniform Rectifiability

Kaj Nyström (Uppsala University)

Abstract:

—–

Title: Basecamp for convergence of ergodic averages along subsequences

Máté Weirdl (The University of Memphis)

Abstract: The purpose of this talk is to give a summary of the ergodic theoretical background for subsequence ergodic theorems (pioneered by von Neumann, Bellow,

The audience is assumed to have a background in real analysis, including Hilbert spaces, but not in ergodic theory.

Summer 2024

Friday 24 May at 2 pm

JCMB 6201

Multilinear and Weighted Estimates for Oscillatory Integral Operators

David Rule (Linköping University)

Abstract: We discuss the classical T1 theorem of David and Journé on the boundedness of Calderón-Zygmund operators and recall some equivalent versions of this result. We also mention a version of the T1 theorem forthe compactness of Calderón-Zygmund operators. The last part of the talk is based on some recent joint work with Guopeng Li (UoE), Tadahiro Oh (UoE) and Rodolfo Torres (UC Riverside). The talk is an introduction to a celebrated result in harmonic analysis and is mostly intended for beginning graduate students in analysis and PDEs.

Thursday 11 July at 3 pm

JCMB 5323

Some Developments in the Eigenvalue Distribution of Spatio-Spectral Limiting Operators in two domains

Azita Mayeli (City University of New York)

Abstract: Let $F$ , $S$ be bounded measurable sets in $\R^d$ . Let $P_F : L^2(\R^d) \rightarrow L^2(\R^d)$ be the orthogonal projection on the subspace of functions with compact support on $F$ , and let $B_S : L^2(\R^d) \rightarrow L^2(\R^d)$ be the orthogonal projection on the subspace of functions with Fourier transforms having compact support on $S$ . We define the \emph{spatio-spectral limiting operator} as a composition of the orthogonal projections $B_S P_F B_S : L^2(\Bbb R^d) \rightarrow L^2(\Bbb R^d)$ .

The non-asymptotic eigenvalue distribution of this operator in dimension $d = 1$ has been studied for the case when $F$ and $S$ are both intervals. In higher dimensions, some asymptotic results are known when $S$ and $F$ are balls, and these results have proved useful for various applications, such as interpolation.

In this talk, I will report on the {\it non-asymptotic} distributional estimates of the eigenvalue sequence of this operator for $d \geq 1$ for more {\it general} spatio and frequency domains $F$ and $S$ , resepectively. The significance of these estimates lies in their diverse applications in wireless communications, medical imaging, signal processing, geophysics, and astronomy.

Spring 2024

Monday, 15 Janurary 2024

JCMB 5323

Variable coefficient Lp local smoothing and applications

Jonathan Hickman (UoE)

Abstract:

I will discuss some work in progress, concerning variable coefficient extensions of Lp local smoothing estimates for the Schrodinger propagator. This can be thought of as a counterpart to a classical oscillatory integral operator bound of Bourgain (1991). Whilst Bourgain’s result relies on studying Kakeya sets of curves, our Lp local smoothing result relies on studying Nikodym sets of curves. An important observation of Wisewell (2005) is that the Nikodym theory is surprisingly different from the Kakeya theory. Our work aims to further investigate and exploit these differences.

Part of an ongoing project, joint with Shaoming Guo, Marina Iliopoulou and Jim Wright.

Wednesday 3.05pm, 24 Janurary 2024

JCMB 5323

Future stability of spatially homogeneous Friedmann–Lemaitre–Robertson–Walker solutions of the Einstein–massless Vlasov system

Martin Taylor (Imperial College London)

Abstract: Spatially homogeneous Friedmann–Lemaitre–Robertson–Walker solutions constitute an infinite dimensional family of cosmological solutions of the Einstein–massless Vlasov system. Each member describes a spatially homogenous universe, filled with massless particles, evolving from a big bang singularity and expanding towards the future at a decelerated rate. I will present a theorem on the future stability of this family to spherically symmetric perturbations.

Monday, 29 Janurary 2024

JCMB 5323

Rectifiability and tangents in a rough Riemannian setting

Max Goering (University of Jyvaskyla)

Abstract: In the 1920s Besicovitch asked the question: What can one say about the structure of sets $E$ in the plane, with the property that $\lim_{r \downarrow 0} \frac{\mathcal{H}^{m}(E \cap B(x,r))}{r^{m}} =1$ for almost every $x \in E$ ? In 1987 Preiss gave a complete answer to Besicovitch’s density question in the setting of measures. This groundbreaking work relies on his introduction of tangent measures. This talk will introduce tangent measures, their properties that make them so widely applicable, and discuss recent joint work with Tatiana Toro and Bobby Wilson where we introduce an anisotropic analog of tangent measures called $\Lambda$ -tangents. I will then discuss applications of $\Lambda$ -tangents to understanding geometric regularity of the support of a measure given analytic properties of the measure and relationships to PDE.

Monday, 5 February 2024

JCMB 5323

Deep-water and shallow-water limits of statistical equilibria for the intermediate long wave equation

Guopeng Li (UoE)

Abstract:

The Intermediate Long Wave equation (ILW) models the internal wave propagation of the interface in a stratified fluid of finite depth, establishing a natural connection between the deep-water regime (the Benjamin-Ono (BO) regime) and the shallow-water regime (the Korteweg-de Vries (KdV) regime). In this talk, I will address convergence issues for ILW from a statistical mechanics viewpoint at different energy levels. By exploiting both the Hamiltonian and completely integrable structure of ILW, BO, and KdV, I will delve into the convergence of Hamiltonian and higher-order conservation laws for ILW, along with their associated measures and dynamics. Two interesting phenomena arise: (i) the modes of convergence of the measures in the deep-water and shallowwater limits differ. (ii) KdV, appearing in the shallow-water limit, possesses half as many conservation laws as ILW and BO, leading to a 2-to-1 collapse phenomenon.

This talk is based on joint works with Tadahiro Oh, Andreia Chapouto (both Edinburgh) and Guangqu Zheng (Liverpool).

Monday, 12 February 2024

JCMB 5323

Elliptic PDE with Hölder data in rough sets

Pablo Hidalgo-Palencia (ICMAT)

Abstract: It has been known already for 100 years, since the work of Wiener, that domains need to satisfy some geometric conditions in order for harmonic functions to attain their boundary values in a continuous way. These geometric conditions in fact turn out to be valid for a much wider class of operators, as Littman, Stampacchia and Weinberger showed later (1963).In this talk, we will explore the quantitative extension of the last result: we will characterize the domains in which the Dirichlet problem with Hölder continuous boundary datum has solutions which arrive to the boundary in the desirable Hölder continuous way. Indeed, we will show that the capacity density condition that Aikawa (2002) showed to be optimal for the Laplacian, in fact works for general elliptic operators with merely bounded coefficients.This is joint work with M. Cao, J.M. Martell, C. Prisuelos-Arribas and Z. Zhao.

Monday, 19 February 2024 (Flexible Learning Week)

Monday, 26 February 2024

JCMB 5323

Stochastic compactness method and the Camassa–Holm equation with gradient noise

Peter H.C. Pang (University of Oslo)

Abstract:

In this talk I intend to give an overview of a general schema for establishing existence of solutions in nonlinear SPDEs, and outline an application to the inviscid limit of the Camassa–Holm equation with gradient noise. The Camassa–Holm equation is a bi-Hamiltonian, nonlocal equation that exhibits non-uniqueness after a particular mode of blow-up known as wave-breaking. This talk is aimed at a general analysis audience, but I shall touch on interesting particulars of this equation and of gradient-type noise. This is primarily based on joint work with Helge Holden (NTNU), Kenneth Karlsen (Oslo), and Luca Galimberti (KCL) (2024, JDE, https://eur02.safelinks.protection.outlook.com/?url=https%3A%2F%2Fdoi.org%2F10.1016%2Fj.jde.2023.12.021&data=05%7C02%7C%7C6e932c03ea474d9b184808dc312acdcc%7C2e9f06b016694589878910a06934dc61%7C0%7C0%7C638439307105225558%7CUnknown%7CTWFpbGZsb3d8eyJWIjoiMC4wLjAwMDAiLCJQIjoiV2luMzIiLCJBTiI6Ik1haWwiLCJXVCI6Mn0%3D%7C0%7C%7C%7C&sdata=edertc5P17u0%2FI6kZDs6%2BikLnm2Axt7rjn7I031lKsk%3D&reserved=0).

Monday, 4 March 2024

JCMB 5323

Global stability of Kaluza-Klein spacetimes

Zoe Wyatt (University of Cambridge)

Abstract: Spacetimes formed from the cartesian product of Minkowski spacetime and a compact space play an important role in supergravity and string theory. In this talk I will discuss a recent joint work with C. Huneau and A. Stingo showing the nonlinear classical stability of such a product spacetime in the case when the compact space is a flat torus. I will also explain how our result is connected to claims of Penrose and Witten.

Monday, 11 March 2024

JCMB 5323

Sharp quasi-invariance threshold for the cubic Szeg\H{o} equation

James Coe (UoE)

Abstract:

In this talk we will discuss recent work on the dynamics of generic solutions to the Cubic Szeg\H{o} equation, a Hamiltonian system serving as a toy model for weakly-dispersive dynamics. We consider a family of Gaussian fields of varying regularity and describe the flow properties of such measures under these dynamics. We shall see that above a critical regularity, the measures are quasi-invariant under the flow, but below this regularity, quasi-invariance fails; in fact the distribution at time t is singular with respect to the initial distribution for almost all times.

We introduce a new method to show singularity, first by exhibiting an instantaneous growth of Sobolev norms of the solution (at high frequencies), and then employing an abstract argument to show that such a property cannot hold with positive probability for many times. We will cover the main ideas in both regimes, proving (relatively) standard energy estimates in the high-regularity setting, and in the low-regularity setting we shall see a general heuristic for when we expect singularity, and justify this for the Szeg\H{o} dynamics by proving sharp deterministic multilinear estimates and introducing a para-controlled approximation.

Friday, 15 March 2024 2pm to 5:20pm

ICMS Lecture Theatre

Maxwell Analysis Mini-Symposium

Grigori Rozenbloum (Chalmers University of Technology, Sweden)

Title: Weyl asymptotics for eigenvalues of Poincare-Steklov problem in a domain with Lipschitz boundary

Abstract: The Poincare-Steklov eigenvalue problem is a second order elliptic equation with spectral parameter in the boundary condition, for example

$-\Delta u(X)+ \mathbf{v}(X)u(X)=0 \text{ in }\Omega\subset\mathbb{R}^{d+1},$

$\lambda\partial_\nu u(X) = p(X)u(X),\, X\in\partial\Omega.$

This problem is presently of high interest both in pure mathematics and applications. One of questions arising around this problem is the asymptotic behavior of eigenvalues. The initial result, for a rather smooth boundary, was obtained in 1955 by L.Sandgren. After this, the conditions on the boundary were being gradually relaxed, but the question about the validity of the asymptotic formula for a Lipschitz boundary stood open and challenging since 2006. The approach by the Author consist in the initial reduction the problem to the one in a smooth domain but with highly irregular coefficients of the equation and further approximation by equations with smooth coefficients. Some ideas in the proof may be interested in the study of other spectral problems.

Susanna Terracini (University of Turin, Italy)

Title: Rotating Spirals in competition-difuision systems

Abstract:Terracini_abstract_maxwell2024

Eugene Shargorodsky (King’s College London)

Title: Variations on Liouville’s theorem

Abstract: A classical theorem of Liouville states that a function that is analytic and bounded on the entire complex plane is in fact constant. The same conclusion is true for a function that is harmonic and bounded on $\mathbb{R}^n$ .
The talk discusses generalisations of Liouville’s theorem to nonlocal translation-invariant operators. It is based on a joint work with D. Berger and R.L. Schilling, and a further joint work with the same co-authors and T. Sharia. We consider operators with continuous but not necessarily infinitely smooth symbols.
It follows from our results that if $\left\{\eta \in \mathbb{R}^n \mid m(\eta) = 0\right\} \subseteq \{0\}$ , then, under suitable conditions, every polynomially bounded weak solution $f$ of the equation $m(D)f=0$ is in fact a polynomial, while sub-exponentially growing solutions admit analytic continuation to entire functions on $\mathbb{C}^n$ .

Monday, 18 March 2024

JCMB 5323

90 years of pointwise ergodic theory

Ben Krause (University of Bristol)

Abstract: In this talk I will discuss the greatest hits in pointwise ergodic theory, beginning with the work of Birkhoff, focusing on that of Bourgain, and concluding with work done post-covid.

Monday, 25 March 2024

JCMB 5323

The Dirac equation in dispersive PDEs: advances and open problems

Federico Cacciafesta(The university of Padova)

Abstract:

The Dirac equation is one of the fundamental equations in relativistic quantum mechanics, widely used in a large number of applications from physics to quantum chemistry. The aim of this talk will be to discuss some recent results, together with a number of open questions, concerning the dynamics for this model: after briefly reviewing the main properties of the Dirac operator and providing some background and motivations from the theory of linear dispersive PDEs, we shall mainly focus onto some scaling critical models, namely the Dirac-Coulomb and the Dirac-Aharonov Bohm equations, showing how some linear estimates (in particular, Strichartz estimates) can be obtained by exploiting the spectral properties of the operator.

Tuesday, 26 March 2024, 2:05 pm

Lecture Theatre B

T1 theorem: boundedness and compactness of Calderón-Zygmund operators

Arpad Benyi (Western Washington University)

Abstract:

We discuss the classical T1 theorem of David and Journé on the boundedness of Calderón-Zygmund operators and recall some equivalent versions of this result. We also mention a version of the T1 theorem forthe compactness of Calderón-Zygmund operators. The last part of the talk is based on some recent joint work with Guopeng Li (UoE), Tadahiro Oh (UoE) and Rodolfo Torres (UC Riverside). The talk is an introduction to a celebrated result in harmonic analysis and is mostly intended for beginning graduate students in analysis and PDEs.

Previous semester

Autumn 2023

Monday, 18th September 2023

Disproving the Deift conjecture: the loss of almost periodicity

Andreia Chapouto (University of Edinburgh)

Abstract: In 2008, Deift conjectured that almost periodic initial data leads to almost periodic solutions to the Korteweg-de Vries equation (KdV). In this talk, we show that this is not always the case. Namely, we construct almost periodic initial data whose KdV evolution remains bounded but loses almost periodicity at a later time, by building on the new observation that the conjecture fails for the Airy equation. This is joint work with Rowan Killip and Monica Visan.

Monday, 25 September 2023

Counterexamples to the typical behaviour of elliptic measures on fractals

Polina Perstneva (Université Paris-Saclay)

Abstract:

Recent developments in Geometric Measure Theory have led to the understanding that, essentially, rectifiability of the boundary of a domain is necessary and sufficient for the harmonic measure to be (qualitatively) absolutely continuous with respect to the Hausdorff measure on that boundary. The counterpart of this is the following: for purely unrectifiable sets, the harmonic measure is singular with respect to the boundary measure.

Recall that a set $E \subset \R^n$ is called $d$ -rectifiable if it can be represented as a union of images of Lipschitz functions $f_i: \mathbb{R}^d \to \mathbb{R}^n$ up to an $\mathcal{H}^d$ -null set. A set $E \subset \mathbb{R}^n$ is purely $d$ -unrectifiable if it is an anti-pod of the previous: its intersection with any image of a Lipschitz function $f: \mathbb{R}^d \to \mathbb{R}^n$ has $\mathcal{H}^d$ measure zero. Classical examples of unrectifiable sets are fractals: on the plane, the famous ones are the Koch snowflake, the four corners Cantor set, the Sierpinski carpet, etc.

It is also known that all the operators close to the Laplacian, which generates the harmonic measure, produce elliptic measures with the same properties as above. However, it turns out that for some unrectifiable sets on the plane there exists an elliptic operator with a scalar coefficient whose elliptic measure behaves in the opposite way than the harmonic measure does. We will discuss these counterexamples discovered in the last couple of years by G. David, S. Mayboroda, and the speaker, and look briefly into some open problems around them.

Wednesday 3 pm, 27 September 2023

JCMB 5326

On elliptic and parabolic PDEs in double divergence form

Seick Kim (Yonsei University)

Abstract:

We consider elliptic operator $L^*$ of the form

$</div> <div>L^* u = \sum_{i,j=1}^d D_{ij}(a^{ij} u)-\sum_{i=1}^d D_i(b^i u) + cu.</div> <div>$

The operator $L^*$ is called double divergence form operator and it is the formal adjoint of the elliptic operator in non-divergence form $L$ given by

$</div> <div>Lv = \sum_{i,j=1}^d a^{ij} D_{ij}u+\sum_{i=1}^d b^i D_i u + cu.</div> <div>$

An important example of a double divergence form equation is the stationary Kolmogorov equation for invariant measures of a diffusion process.

We are concerned with regularity of weak solutions of $L^* u=0$ and show that Schauder type estimates are available when the coefficients are of Dini mean oscillation and $b^i$ and $c$ belong to certain function spaces.

We will also discuss some applications and parabolic counterparts.

Monday, 02 October 2023

JCMB 5323

Global well-posedness and quasi-invariance of Gaussian measures for fractional nonlinear Schrödinger equations,

Justin Forlano (University of Edinburgh)

Abstract:

In this talk, we discuss the long-time dynamics and statistical properties of solutions to the cubic fractional nonlinear Schrödinger equation (FNLS) on the one-dimensional torus, with Gaussian initial data of negative regularity. We prove that FNLS is almost surely globally well-posed and the associated Gaussian measure is quasi-invariant under the flow. In lower-dispersion settings, the regularity of the initial data is below that amenable to the deterministic well-posedness theory. In our approach, inspired by the seminal work by DiPerna-Lions (1989), we shift attention from the flow of FNLS to controlling solutions to the infinite-dimensional Liouville equation of the transported Gaussian measure. We establish suitable bounds in this setting, which we then transfer back to the equation by adapting Bourgain’s invariant measure argument to quasi-invariant measures.

This is a joint work with Leonardo Tolomeo (University of Edinburgh).

Monday, 09 October 2023

JCMB 5323

Assouad dimension and tangents of dynamically invariant sets

Alex Rutar (University of St. Andrews)

Abstract:

A tangent of a compact set is an accumulation point in Hausdorff distance given by ‘zooming in’ at a given point. For general compact sets, it is well-known that the Assouad dimension is characterized by dimensions of weak tangents (where the location of zooming in is allowed to change), but not necessarily characterized by tangents. However, for sets satisfying some form of dynamical invariance, it is reasonable to expect that more can be said. In fact, one would hope that most points have tangents that are as large as possible. I will discuss such phenomena in general, and for some particular families of sets which arise as attractors of iterated function systems. This is based on joint work with Antti Käenmäki (University of Oulu).

Monday, 16 October 2023

JCMB 5323

A semiclassical trace norm bound on certain commutators

Søren Mikkelsen

Abstract:

In a series of papers N. Benedikter, M. Porta and B. Schlein considered time evolution of systems of elementary particles (fermions). In these studies, they were able to describe how the particles evolve in time in certain settings given some initial state of the system. One assumption on the initial state was concerning a semiclassical bound on certain commutators. A mean-field version of this bound takes the form

$\big\lVert [ A, \boldsymbol{1}_{(-\infty,0]}(H_\hbar) ] \big\rVert_1 \leq C\hbar^{1-d},$

where $H_\hbar = -\hbar^2\Delta +V$ is a Schrödinger operator, $A$ is either the position operator $X$ or the momentum operator $-i\hbar\nabla$ , $C$ is a positive constant and $\lVert\cdot\rVert_{1}$ denotes the trace norm. In this talk we will discuss ideas and methods used in a proof of such semiclassical commutator bounds.

Monday, 23 October 2023

JCMB 5323

Weak turbulence on Schwarzschild-AdS spacetime

Georgios Moschidis (EPFL)

Abstract:

n the presence of confinement, the Einstein field equations are expected to exhibit turbulent dynamics. The simplest example of such behaviour is described by the AdS instability conjecture, put forward by Dafermos and Holzegel in 2006; this conjecture suggests that generic small perturbations of the AdS initial data lead to the formation of trapped surfaces when reflecting boundary conditions are imposed at conformal infinity. However, whether a similar scenario also holds in the more complicated case of the exterior region of an asymptotically AdS black hole spacetime has been the subject of debate.

In this talk, we will show that weak turbulence does emerge in the dynamics of a quasilinear toy model for the vacuum Einstein equations on the Schwarzschild-AdS exterior spacetimes for an open and dense set of black hole mass parameters. This is joint work with Christoph Kehle.

Monday, 30 October 2023

JCMB 5323

A Kakeya maximal function in the (first) Heisenberg group

Pietro Wald (University of Warwick)

Abstract:

The Kakeya conjecture is a prominent open problem in analysis, sitting at the intersection of geometric measure theory, harmonic analysis, and PDE.

In this talk, I will introduce the (first) Heisenberg group and a notion of Kakeya set in this setting. I will then discuss the corresponding Kakeya conjecture (first solved by J. Liu) and present a new solution based on a suitable adaptation of the Kakeya maximal function to the Heisenberg group. This is based on joint work with K. Fässler and A. Pinamonti.

Friday, 3 November 2023

JCMB 5323

Maxwell Analysis Mini-Symposium

Lucio Galeati (EPFL)

Regularisation by transport noise for 2D fluid dynamics equations

Abstract: A major question in fluid dynamics is to understand whether solutions to 2D incompressible Euler equations with $L^p$ -valued vorticity are unique, for some $p\in [1,\infty)$ . A related problem, more probabilistic in flavour, is whether one can find a physically meaningful noise restoring well-posedness of the PDE.
In this talk I will present some recent advances on the latter, for a class of slightly regularised 2D Euler-type equations (specifically, logEuler and hypodissipative Navier-Stokes), in the presence of a rough Kraichnan-type noise, modelling the small scales of a turbulent fluid; uniqueness in law can then be shown for solutions with $L^2$ -valued vorticity.
Based on a joint work with Dejun Luo (Beijing).

Joan Verdera (UAB)

Explicit minimisers of non-local energies

Abstract: Abstract_Verdera_Edinburgh.pdf

Monday, 13 November 2023

JCMB 5323

Singular integrals in Banach function spaces

Zoe Nieraeth (she/her), (Basque Center for Applied Mathematics)

Abstract: Singular integrals arise when studying properties of the solution of a given PDE by applying them to the initial data. Classically, this was studied for data belonging to weighted Lebesgue spaces. However, this is not always the right setting for every problem. For example, in recent years problems involving non-homogeneous data have been studied through weighted variable Lebesgue spaces, and elliptic boundary value problems through weighted Morrey spaces. These spaces are examples of the generalized notion of Banach function spaces. In this talk I will discuss a unification and extension to a limited range setting of some results classically studied for weighted Lebesgue spaces, such as the Rubio de Francia extrapolation theorem, through this general framework. I will also discuss an application to compact extrapolation that is part of a joint work with Emiel Lorist.

Wednesday, 22 November 2023

Newhaven Lecture Theatre, 15 South College Street, 2:30pm – 5pm

Joint Maxwell Analysis Seminar

Shape Optimisation for nonlocal anisotropic energies

Lucia Scardia (Heriot-Watt)

Abstract: TBC

The Euclidean 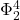$\Phi^4_2$ theory as the limit of an interacting Bose gas

Vedran Sohinger (Warwick)

Abstract: Gibbs measures of nonlinear Schrödinger equations are a fundamental object used to study low-regularity solutions with random initial data. In the dispersive PDE community, this point of view was pioneered by Bourgain in the 1990s. On the other hand, the nonlinear Schrödinger equation can be viewed a classical limit of many-body quantum theory. We are interested in the problem of the derivation of Gibbs measures as mean-field limits of Gibbs states in many-body quantum mechanics.

The particular case we consider is when the dimension d=2 and when the interaction potential is the delta function, which corresponds to the Euclidean $\Phi^4_2$ theory. The limit that we consider corresponds to taking the density to be large and the range of the interaction to be small in a controlled way. Our proof is based on two main ingredients.
(a) An infinite-dimensional stationary phase argument, based on a functional integral representation.
(b) A Nelson-type estimate for a nonlocal field theory in two dimensions.

This is joint work with J.Fröhlich, A. Knowles, and B. Schlein.

Monday, 27 November 2023

JCMB 5323

Heat flow regularisation, Brascamp—Lieb inequality, and convex
geometry

Shohei Nakamura (Birmingham & Osaka)

Abstract:This talk is based on the joint work with Hiroshi Tsuji (Osaka, Japan).
A close link between Brascamp—Lieb inequality and convex geometry was discovered by Kieth Ball; volume ratio estimate, reverse isoperimetric problem, Buseman-Petty problem etc.
In this talk we will report further link to the volume product of a convex body (Blaschke—Santaló inequality and Mahler’s conjecture).
Our principal observation is to understand the volume product as a regularising effect of the Ornstein—Uhlenbeck heat flow (hypercontractivity) which is one of archetype example of Brascamp—Lieb inequality. We then exhibit a wealth of this new link.

Thursday, 7 December 2023

JCMB 5323

Hyperbolic sine-Gordon model beyond the first threshold

Younes Zine (EPFL)

Abstract: Over the last twenty years there has been significant progress in the well-posedness study of singular random dispersive PDEs with polynomial nonlinearities. The scenario when the nonlinearity is non-polynomial is however still poorly understood. The objective of this talk is to discuss recent progress in this direction. More precisely, I will discuss a joint work with T. Oh (Edinburgh) where we improve on the well-posedness issue for the hyperbolic sine-Gordon model introduced by Oh, Robert, Sosoe and Wang (2021). This model corresponds to the two-dimensional damped wave equation with the sine nonlinearity, forced by an additive space-time white noise.

I will first briefly review the well-posedness issue for singular stochastic wave equations with polynomial nonlinearities and explain why the tools and methods developed for their study are not applicable to the sine-Gordon equation at hand. I will then introduce a novel analytical setup, which we call the physical Fourier restriction norm method, that is well-suited for the study of random wave equations with non-polynomial nonlinearities. In particular, I will describe how, in this setting, the recent resolution of the three-dimensional cone multiplier conjecture by Guth, Wang and Zhang (2019) allows us to prove key deterministic bilinear estimates.

In the second part of the talk, I will provide details on the proof of the so-called nonlinear smoothing for the imaginary Gaussian multiplicative chaos, within the framework of the physical Fourier restriction norm method. This constitutes the main probabilistic step in our argument.

Spring 2023

Monday, 16 Jan 2023

Hyperbolic P(\Phi)_2 model on the plane

Hiro Oh (University of Edinburgh)

Abstract:I will discuss well-posedness of the stochastic damped nonlinear wave equation (SdNLW) forced by a space-time white noise with the Gibbsian initial data. This problem is also known as the hyperbolic $\Phi^{k+1}_2$ -model since it corresponds to the so-called canonical stochastic quantization of the $\Phi^{k+1}_2$ -measure. In this talk, our main goal is to study this problem on the plane.

I will first go over the well-posedness result on the two-dimensional torus studied by Gubinelli-Koch-Oh-Tolomeo (2022). Then, by taking a large torus limit, I aim to construct invariant Gibbs dynamics for the hyperbolic $\Phi^{k+1}_2$ -model on the plane.

In taking a large torus limit, I will discuss

(i) the construction of a $\Phi^{k+1}_2$ -measure on the plane as a limit of the $\Phi^{k+1}_2$ -measures on large tori. This is done by establishing coming-down-from-infinity for the associated stochastic nonlinear heat equation (SNLH) on the plane.

(ii) the construction of invariant Gibbs dynamics for the hyperbolic $\Phi^{k+1}_2$ -model on the plane by taking a limit of the invariant Gibbs dynamics on large tori. Our strategy is inspired by a recent work by Oh-Okamoto-Tolomeo (2021) on the hyperbolic $\Phi^3_3$ -model on the three-dimensional torus, where we reduce the problem to studying convergence of the so-called enhanced Gibbs measures. By combining wave and heat analysis together with ideas from optimal transport theory, I establish convergence of the enhanced Gibbs measures.

This talk is based on a joint work with Leonardo Tolomeo (The University of Edinburgh), Yuzhao Wang (University of Birmingham), and Guangqu Zheng (University of Liverpool).

Monday, 30 Jan 2023

Local well-posedness of a quadratic nonlinear Schrödinger equation on the two-dimensional torus.

Ruoyuan Liu (University of Edinburgh)

Abstract: In this talk, I will present results on local well-posedness of the nonlinear Schrödinger equation (NLS) with the quadratic nonlinearity |u|^2, posed on the two-dimensional torus, from both determinstic and probabilistic points of view.

For the deterministic well-posedness, Bourgain (1993) proved local well-posedness of the quadratic NLS in H^s for any s > 0. In this talk, I will go over local well-posedness in L^2, thus resolving an open problem of 30 years since Bourgain (1993). In terms of ill-posedness in negative Sobolev spaces, this result is sharp. As a corollary, a multilinear version of the conjectural L^3-Strichartz estimate on the two-dimensional torus is obtained.

For the probabilistic well-posedness, I will talk about almost sure local well-posedness of the quadratic NLS with random initial data distributed according to a fractional derivative of the Gaussian free field, and also a certain probabilistic ill-posedness result when the initial data becomes very rough. In particular, this part of the talk shows that the prediction on the critical regularity made by the probabilistic scaling due to Deng, Nahmod, and Yue (2019) breaks down for this model.

The first part of the talk is based on a joint work with Tadahiro Oh (The University of Edinburgh).

Monday, 6 Feb 2023

Magnitude, diversity, homology

Emily Roff (University of Edinburgh)

Abstract: Magnitude is an isometric invariant of metric spaces, usually interpreted as assigning to each space a real-valued function on the positive half-line. Though its provenance is category-theoretic, the magnitude function of a compact metric space turns out to be a geometrically rich invariant, its asymptotics carrying subtle information about the intrinsic volumes of a space and the Willmore energy.

In recent years there have been rapid advances in our understanding of the magnitude function, particularly for submanifolds of Euclidean space—yet, many interesting questions still stand open. This talk will introduce the theory and survey recent results due to Gimperlein, Goffeng, Louca and Meckes. I will also describe aspects of my own work, joint with Leinster and extending results due to Leinster and Meckes, which link the study of magnitude to problems in the quantification of ecological diversity. Finally, I will sketch the connection to magnitude homology, an algebraic invariant designed to `categorify’ the magnitude function. Throughout, I will foreground open questions of an analytic nature.

Monday, 13 Feb 2023

Microscopic derivation of Gibbs measures for the 1D focusing nonlinear Schrödinger equation

Andrew Rout (University of Warwick)

Abstract: Gibbs measures for the nonlinear Schrödinger equation (NLS) are important objects used to study low-regularity almost sure well-posedness. On the other hand, the NLS can be viewed as a limit of many-body quantum mechanics. In this talk we describe the derivation of Gibbs measures from their many-body quantum analogues.In particular, we consider dimension d=1 with a non-positive interaction potential. The proof is based off a perturbative expansion of the Hamiltonian and a diagrammatic representation of the interaction.

This is based on joint work with Vedran Sohinger.

Monday, 20 Feb 2023

A sharp Fourier extension inequality on the circle under arithmetic constraints

Valentina Ciccone (Universität Bonn)

Abstract:In this talk, we discuss a sharp Fourier extension inequality on the circle in the Stein-Tomas endpoint case for functions whose spectrum satisfies a certain arithmetic constraint. Such arithmetic constraint corresponds to a generalization of the notion of $B_3$ -set.

This talk is based on a joint work with Felipe Gonçalves.

Monday, 6 March 2023

Boundary preimages of linear combinations of iterates of Blaschke products

Spyridon Kakaroumpas (University of Würzburg)

Abstract:

Let $f$ be a finite Blaschke product on the unit disk with $f(0)=0$ that is not a rotation. Motivated by earlier results of M.~Weiss on lacunary power series, J.~J.~Donaire and A.~Nicolau proved that if $(a_n)^{\infty}_{n=1}$ is a sequence of complex numbers such that $\lim_{n\rightarrow\infty}a_n=0$ and $\sum_{n=1}^{\infty}|a_n|=\infty$ , then for all $w\in\mathbb{C}$ , there exists $\xi\in\mathbb{D}$ such that $\sum_{n=1}^{\infty}a_nf^{n}(\xi)=w$ , where $f^n$ denotes the $n$ -th iterate of $f$ (i.~e.~its composition with itself $n$ times).

In this talk we discuss an extension of this result, which shows that under the same conditions on the coefficients $(a_n)^{\infty}_{n=1}$ , the set $E$ of all $\xi\in\mathbb{D}$ such that $\sum_{n=1}^{\infty}a_nf^n(\xi)=w$ has Hausdorff dimension 1. We use an iterative construction of appropriate Cantor-type sets, which depends on a careful analysis of the machinery developed by Donaire–Nicolau.

We also explore the optimality of our result under imposing more restrictive conditions on the coefficients $(a_n)^{\infty}_{n=1}$ . On the one hand, for any fixed gauge function $\varphi$ that is “better” than any power function, we provide conditions which ensure that the set $E$ has positive $\varphi$ -Hausdorff content. On the other hand, we also provide conditions which ensure that $E$ has zero $\varphi$ -Hausdorff content, in the important special case that the Blaschke product $f$ is of the form $f(z)=z^m$ .

This is joint work with O.~Soler i Gibert.

Monday, 13 March 2023

Dimensions of infinitely generated self-conformal sets

Amlan Banaji (Loughborough University)

Abstract: Many fractals can be realised as the limit set of an iterated function system (IFS) of contracting maps. If the IFS consists of a countably infinite number of maps, then different notions of fractal dimension of the resulting limit set, such as Hausdorff, box and Assouad-type dimensions, can take different values, even if the contractions are assumed to be conformal and well-separated. We will explain what is known about these dimensions in this setting, and describe applications to parabolic Cantor sets, and to sets of numbers which have continued fraction expansions with restricted entries. This talk is based on joint work with Jonathan Fraser.

Monday, 27 March 2023

Solvability of the Poisson problem with interior data in 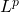$L^p$ Carleson spaces and its applications to the regularity problem.

Bruno Poggi Cevallos (Universitat Autònoma de Barcelona)

Abstract: On Corkscrew domains with Ahlfors-regular boundary, we prove the equivalence of the classically considered $L^p$ -solvability of the (homogeneous) Dirichlet problem with the solvability of the inhomogeneous Poisson problem with interior data in an $L^p$ -Carleson space (with a natural bound on the $L^p$ norm of the non-tangential maximal function of the solution), and we study several applications. Our main application is towards the $L^q$ Dirichlet-regularity problem for second-order elliptic operators satisfying the Dahlberg-Kenig-Pipher condition (this is, roughly speaking, a Carleson measure condition on the square of the gradient of the coefficients), in the geometric generality of bounded Corkscrew domains with uniformly rectifiable boundaries (although this problem had been open even in the unit ball). Other applications include: several new characterizations of the $L^p$ -solvability of the Dirichlet problem, new non-tangential maximal function estimates for the Green’s function, a new local T1-type theorem for the $L^p$ solvability of the Dirichlet problem, new estimates for eigenfunctions, free boundary theorems, and a bridge to the theory of the Filoche-Mayboroda landscape function (also known as torsion function). This is joint work with Mihalis Mourgoglou and Xavier Tolsa.

Friday, 31 March 2023, 14:00 – 17:30, Appleton Tower Lecture Theatre 3

Maxwell Mini-Symposium in Harmonic Analysis and PDE

https://www.maths.ed.ac.uk/~toh/Files/2023MI/MI03_2023.html

Nicolas Burq (Universite Paris-Saclay and Institut Universitaire de France),

Mathieu Lewin (CNRS and Universite Paris Dauphine, France),

Maciej Zworski (UC Berkeley, USA)

14:00 – 14:50: Nicolas Burq (Université Paris-Saclay and Institut Universitaire de France)

Title: Propagation of Smallness, Control and Stabilisation

Abstract: Control and stabilization are now well understood when controls or damping act on open sets. When they act on measurable sets only, much remains to be understood. In this talk I will present results in this direction. In most cases (but not always) the results I will present will rely on the quantitative results of Logunov/Malinnikova for harmonic functions that can be translated into control or stabilisation results for heat, waves or Schrodinger equations. Most of the results presented in the talk are in collaboration with I. Moyano (Univ. Nice).

15:00 – 15:50: Mathieu Lewin (CNRS and Université Paris Dauphine, France)

Title: Derivation of nonlinear Gibbs measures from many-body quantum mechanics

Abstract: In this talk, I will define and discuss some probability measures in infinite dimensions, which play an important role in (S)PDE, in Quantum Field Theory and for the description of Bose-Einstein condensates. Those are Gibbs measures associated with nonlinear Schrodinger-type energies. In dimensions larger than or equal to 2, the measures concentrate on distributions, and they need to be properly renormalized. After presenting the Gibbs measures, I will explain how to derive them from many-body quantum mechanics. Joint works with Phan Thanh Nam (Munich) and Nicolas Rougerie (Lyon).

16:30 – 17:20: Maciej Zworski (University of California at Berkeley, USA)

Title: Mathematics of magic angles

Abstract: Magic angles are a hot topic in condensed matter physics: when two sheets of graphene are twisted by those angles the resulting material is superconducting. I will present a very simple operator whose spectral properties are thought to determine which angles are magical. It comes from a 2019 PR Letter by Tarnopolsky–Kruchkov–Vishwanath. The mathematics behind this is an elementary blend of representation theory (of the Heisenberg group in characteristic three), Jacobi theta functions and spectral instability of non-self-adjoint operators (involving Hormander’s bracket condition in a very simple setting). Recent mathematical progress also includes the proof of existence of generalized magic angles and computer assisted proofs of existence of real ones (Luskin–Watson, 2021). The results will be illustrated by colourful numerics which suggest many open problems (joint work with S Becker, M Embree, J Wittsten in 2020 and S Becker, T Humbert and M Hitrik in 2022).

Monday, 3 April 2023, 2.05pm

Retiring the third law of black hole thermodynamics

Ryan Unger (Princeton University)

Abstract: In this talk I will present a rigorous construction of examples of black hole formation which are exactly isometric to extremal Reissner–Nordström after finite time. In particular, our result can be viewed as a definitive disproof of the “third law of black hole thermodynamics.” This is joint work with Christoph Kehle.

Monday, 3 April 2023, 3.00pm JCMB_Lecture Theatre B

The modified Korteweg-de Vries flow around self-similar solutions:large-time asymptotics and blow-up stability

Simão Correia (Instituto Superior Técnico)

Abstract: Self-similar solutions for the modified Korteweg-de Vries equation areof both physical and mathematical interest. On the physical side, amongseveral applications, they model the formation of sharp corners inplanar vortex patches. Mathematically, they describe the asymptoticbehavior of solutions for large times and present a blow-up behavior atthe initial time. Due to their scaling invariance, these solutionsdisplay several critical features (time decay, spatial decay andregularity), which means that the existing theory is not applicable. Inthis talk, I will show that one can define the flow around thesesolutions in order to analyze both the long-time and the blow-upasymptotics. Afterwards, I will present a stability result at theblow-up time and discuss future developments. This is joint work with R.Côte and L. Vega.

Friday, 21 April 2023 from 2.00 p.m, Saturday 22nd April 2023 from 9.30.a.m, George Square area

North British Functional Analysis Seminar meeting

TBA

Maria Jesus Carro (Universidad Complutense de Madrid)

Abstract: TBA

TBA

Cristina Camara (IST Lisboa)

Abstract: TBA

Summer 2023

Monday, 24 April 2023

Harmonic measure on Cantor sets in the plane

Antoine Julia (Université Paris-Saclay)

Abstract: I will present three definitions of harmonic measure in plane domains, and discuss the relationship between the regularity of the harmonic measure and that of the domain. In particular I will explain how one can construct an irregular domain (the complement of a certain Cantor set) for which the harmonic measure is regular. This is based on joint work with Guy David and Cole Jeznach.

Monday, 1 May 2023

Green functions, smooth distances, and uniform rectifiability.

Joseph Feneuil (Australian National University)

Abstract:

The past 10 years have seen considerable achievements at the intersection of harmonic analysis, PDE, and geometric measure theory. One now better understands the relationship between the geometry of the boundary of a domain and the regularity of harmonic/elliptic solutions inside the domain. For instance, it was proved that the uniform rectifiability (UR) of a codimension 1 set is characterized by the $A_\infty$ -absolute continuity of its harmonic measure with respect to the surface measure – or equivalently the solvability of a $L^p$ Dirichlet problem in the complement.

In this talk, I will show that another characterization of UR sets of codimension 1 can be obtained by comparing Green function $G$ with some regularized version of the distance to the boundary. Moreover, I will obtain a characterization of any UR set of any codimension by an estimate on $\nabla|\nabla G|$ . Those are joint works with Guy David, Linhan Li, and Svitlana Mayboroda.

Thursday 1st June 2023, 4.p.m.

JCMB 5323

Dualities on sets and how they appear in optimal transport

Katarzyna Wyczesany

Abstract: In this talk, we will discuss order reversing quasi involutions, which are dualities on their image, and their properties. We prove that any order reversing quasi-involution is of a special form, which arose from the consideration of optimal transport problem with respect to costs that attain infinite values. We will discuss how this unified point of view on order reversing quasi-involutions helps to deeper the understanding of the underlying structures and principles. We will provide many examples and ways to construct new order reversing quasi-involutions from given ones. This talk is based on joint work with Shiri Artstein-Avidan and Shay Sadovsky.

Previous Semester

Autumn 2022

Monday, 26 September 2022

On the boundedness of maximal singular bilinear operators

Arpad Benyi (Western Washington University)

Abstract: We will begin with an outline of the general setting and the history of several operators of interest in harmonic analysis. Then, we will discuss the continuity of some operators stemming from a maximally modulated bilinear Hilbert transform along a cubic curve.

Monday, 03 October 2022

Convergence problems for singular stochastic dynamics

Younes Zine (University of Edinburgh)

Abstract: Over the last twenty years there has been significant progress in the well-posedness study of singular stochastic PDEs in both parabolic and dispersive settings. In this talk, I will discuss some convergence problems for singular stochastic nonlinear PDEs. In a seminal work, Da Prato and Debussche (2003) established well-posedness of the stochastic quantization equation, also known as the parabolic Φ^k+1₂-model in the two-dimensional case. More recently, Gubinelli, Koch, Oh, and Tolomeo proved the corresponding well-posedness for the canonical stochastic quantization equation, also known as the hyperbolic Φ^k+1₂-model in the two-dimensional case. In the first part of this talk, I will describe convergence of the hyperbolic Φ^k+1₂-model to the parabolic Φ^k+1₂-model. In the dispersive setting, Bourgain (1996) established well-posedness for the dispersive Φ⁴₂-model (=deterministic cubic nonlinear Schrödinger equation) on the two-dimensional torus with Gibbsian initial data. In the second part of the talk, I will discuss the convergence of the stochastic complex Ginzburg-Landau equation (= complex-valued version of the parabolic Φ⁴₂-model) to the dispersive Φ⁴₂-model at statistical equilibrium.

Monday, 10 October 2022

A new approach to the Fourier extension problem for the paraboloid.

Itamar Oliveira (Université de Nantes )

Abstract: In this talk we will propose a new way of using lower dimensional information to obtain higher dimensional ones in the context of the Fourier restriction/extension problem. We will focus on the simplest multilinear case, which is the bilinear problem for functions in 2 variables supported in disjoint caps of the paraboloid; in this setting, we will recover Tao’s $L^2 \times L^2$ into $L^{5/3+\varepsilon}$ bound assuming that one of the functions is a tensor. Broadly speaking, the proof depends on carefully combining a vector-valued version of the one-dimensional analog result ( $L^2 \times L^2$ into $L^2$ ) and curvature considerations. If time allows, we will talk about the $k$ -linear problem for $k>2$ , where the method achieves the conjectured exponent up to the endpoint assuming one tensor structure, but now under weak transversality rather than classical transversality.

Monday, 17 October 2022

The 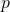$p$ -adic Kakeya conjecture

Bodan Arsovski (UCL)

Abstract: In this talk, we prove the natural analogue of the Kakeya conjecture in the alternative ambient space $\mathbb{Q}_p^n$ , and we discuss some philosophical similarities and differences between this variant of the Kakeya conjecture and the classical Kakeya conjecture in $\mathbb{R}^n$ .

Monday, 24 October 2022

Deriving effective PDEs from many-body Schrödinger equations

Jinyeop Lee (LMU Munich)

Abstract: In this talk, we derive effective dynamics governed by PDEs (nonlinear Schrodinger equation, Vlasov-Poisson equation) from the N-body Schrödinger equation with interactions in the large N limit. For the derivation, we first visit quantum mechanics. Then, using the knowledge of many-body quantum mechanics given in the talk and the suitable conditions for each situation, we derive PDEs describing the effective motion of the system.

Friday, 4 November 14:00 — 17:40, Newhaven Lecture Theatre (13-15 South College Street)

Maxwell Analysis Mini-Symposium

Matteo Capoferri (HW), Jan Sbierski (UoE), Leonardo Tolomeo (UoE), Jiawei Li (UoE)

14:00-14:40 Matteo Capoferri: Spectral theory of systems of PDEs

14:50-15:30 Jan Sbierski: On the uniqueness problem for extensions of Lorentzian manifolds

15:35-16:05 Coffee break

16:05-16:45 Leonardo Tolomeo: Phase transitions of the focusing Φ^p_1 measures

16:55-17:35 Jiawei Li: On distributions of random fields in turbulent flows

Matteo Capoferri:

Title: Spectral theory of systems of PDEs

Abstract: I will present a new approach to the spectral theory of systems of PDEs on closed manifolds, developed in a series of recent papers by Dmitri Vassiliev (UCL) and myself, based on the use of pseudodifferential projections. Emphasis will be placed on ideas and motivation; the talk will include a brief historical overview of the development of the subject area.

Jan Sbierski:

Title: On the uniqueness problem for extensions of Lorentzian manifolds

Abstract: This talk discusses the problem under what conditions two extensions of a Lorentzian manifold have to be the same at the boundary. As will be explained, this question arises naturally in the analysis of Einstein’s equations of general relativity. After making precise the notion of two extensions agreeing at the boundary, we recall a classical example that shows that even under the assumption of analyticity of the extensions, uniqueness at the boundary is in general false — in stark contrast to the extension problem for functions on Euclidean space. We proceed by presenting a recent result that gives a necessary condition for two extensions with at least Lipschitz continuous metrics to agree at the boundary. Furthermore, we discuss the relation to a previous result by Chruściel and demonstrate a new non-uniqueness mechanism for extensions below Lipschitz regularity.

Leonardo Tolomeo:

Title: Phase transitions of the focusing Φ^p_1 measures

Abstract: We study the behaviour of invariant measures for the focusing nonlinear Schrödinger equation on the one-dimensional torus, initiated by Lebowitz, Rose, and Speer (1988). Because of the focusing nature of the measure, it is necessary to introduce a mass cutoff K, and restrict the measure to the set where the mass is smaller than K. We will show the following phase transitions:

– When K is smaller than a certain threshold, the measure is well defined, while for K bigger than the threshold, the measure becomes non-normalisable. We will also discuss what happens at the optimal threshold, and show that the measure is well defined in this case as well, solving a long-standing open problem. This is a joint work with T. Oh (University of Edinburgh) and P. Sosoe (Cornell University).

– When the size L of the torus is going to infinity, in the weakly non-linear regime, numeric simulations in the original paper by Lebowitz, Rose, and Speer (1988) suggest a phase transition depending on the temperature of the system. We show that this is indeed the case: if the temperature is high, the measure converges to a given gaussian measure. However, this convergence does not happen in the low-temperature regime, and instead the measure progressively concentrates around a single soliton. This is a joint work with H. Weber (University of Münster).

Jiawei Li:

Title: On distributions of random fields in turbulent flows

Abstract: In this talk, we are interested in the vorticity and velocity random fields of turbulent flows. I will introduce the evolution equations for probability density functions of these random fields under some conditions on the flow. I will also talk about several methods we used to solve these PDF PDEs numerically. Based on joint works with Zhongmin Qian and Mingrui Zhou.

Monday, 7 November 2022

Hausdorff dimension of self-projective sets

Natalia Jurga (University of St Andrews)

Abstract: A finite set of matrices $A \subset SL(2,R)$ acts on one-dimensional real projective space $RP^1$ through its linear action on $R^2$ . In this talk we will be interested in the limit set of $A$ : the smallest closed subset of $RP^1$ which contains all attracting fixed points of matrices belonging to the semigroup generated by $A$ . This talk will be a gentle introduction to various topics connected to the study of the geometry of these sets and we will discuss recent results concerning their Hausdorff dimension.

Monday, 14 November 2022

Jennifer Duncan (University of Birmingham)

Transversality in Harmonic Analysis and the Brascamp–Lieb Inequalities

Abstract: In modern harmonic analysis, there is a ubiquity of operators whose functional-analytic properties depend on the geometric properties of an underlying submanifold, such as Fourier extension operators and Radon-like transforms. In the analysis of the boundedness of such operators, it is often useful to employ a linear-to-multilinear reduction so that one may appeal to a multilinearised version of the linear estimate one would like to obtain. These multilinear estimates usually require that the submanifolds involved are uniformly transversal in some suitable sense, however, standard linear algebra tools are sometimes insufficient to capture an appropriately general notion of transversality for the estimates in which we are interested. Brascamp–Lieb inequalities offer a robust framework for understanding this higher-order notion transversality in a manner that is well-suited to applications in harmonic analysis. In my talk, I shall introduce the notion of a Brascamp–Lieb inequality, describe the broader role they play in the subject, and go on to discuss the topic of nonlinear Brascamp–Lieb inequalities, a recent variant that generalises this framework to the manifold setting.

Monday, 21 November 2022

Obstruction-free gluing for the Einstein equations

Stefan Czimek (Leipzig University)

Abstract: We present a new approach to the gluing problem in General Relativity, that is, the problem of matching two solutions of the Einstein equations along a spacelike or characteristic (null) hypersurface. In contrast to previous constructions, the new perspective actively utilizes the nonlinearity of the constraint equations. As a result, we are able to remove the 10-dimensional spaces of obstructions to gluing present in the literature. As application, we show that any asymptotically flat spacelike initial data set can be glued to Schwarzschild initial data of sufficiently large mass. This is joint work with I. Rodnianski.

Monday, 28 November 2022

On the extension of surjective operators and its applications

Lenny Neyt (Ghent University)

Abstract: We discuss necessary and sufficient conditions for when the surjectivity of a continuous linear operator between two locally convex spaces implies the surjectivity of the tensorized operator with some topological vector space. This is done via the presence of certain deep topological invariants on the kernel and the vector space, stemming from the application of tools from homological algebra into the field of functional analysis. As an application of these results we discuss the parameter dependence of solutions to partial differential equations and vector-valued extensions of Eidelheit sequences.

Monday, 5 December 2022, JCMB 5328, 2.05pm – 4.00pm

Some probabilistic approaches to NLS in Euclidean space

Nicolas Camps

Abstract: Following the seminal works of Bourgain (1996), and Burq, Tzvetkov (2008), a statistical approach to nonlinear dispersive equations has developed in various contexts. One aspect of the theory is to generate full-measure sets of initial data that lead to strong solutions in certain regimes where instabilities are known to occur.

We discuss the probabilistic Cauchy theory in supercritical regimes for NLS in Euclidean space developed by Bényi, Oh, and Pocovnicu in 2015. In contrast, we proved with Louise Gassot that the pathological set —consisting of initial data that undergoes norm inflation— contains a dense G-delta set. This result is inspired by a construction of Lebeau (2001) and Sun-Tzvetkov (2019) for nonlinear wave equations.

The second part is devoted to the case of weakly dispersive equations in quasi-linear regimes, where the standard probabilistic Cauchy theory fails. We present recent developments based on a paracontrolled ansatz due to Bringmann (2019), which we exploit to prove almost-sure local well-posedness for a class of weakly dispersive equations such as the half-wave equation and the Szego equations. This last result is obtained in collaboration with Louise Gassot and Slim Ibrahim.

Zero-dispersion limit for the Benjamin-Ono equation on the torus

Louise Gassot (University of Basel)

Abstract:We discuss the zero-dispersion limit for the Benjamin-Ono equation on the torus given a bell-shaped initial data. We prove that the solutions admit a weak limit as the dispersion parameter tends to zero, which is explicit and constructed from the Burgers’ equation. The approach relies on the complete integrability for the Benjamin-Ono equation from Gérard, Kappeler and Topalov, and also on the spectral study of the Lax operator associated to the initial data in the zero-dispersion limit.

Summer 2022

Friday, 29 April 2022

Spectrum of the Maxwell Equations for the Flat Interface between Homogeneous Dispersive Media

Ian Wood (University of Kent)

(Virtual Maxwell Analysis Seminar)

Abstract:

We determine and classify the spectrum of a non-selfadjoint operator pencil generated by the time-harmonic Maxwell problem with a nonlinear dependence on the frequency. More specifically, we consider one- and two-dimensional reductions for the case of two homogeneous materials joined at a planar interface. The dependence on the spectral parameter, i.e. the frequency, is in the dielectric function and we make no assumptions on its form. In order to allow also for non-conservative media, the dielectric function is allowed to be complex, yielding a non-selfadjoint problem. This is joint work with Malcolm Brown (Cardiff), Tomas Dohnal (Halle) and Michael Plum (Karlsruhe).

Friday, 13 May 2022

Generated Jacobian equations and applications to nonimaging optics

Boris Thibert (Universite Grenoble Alpes)

(Virtual Maxwell Analysis Seminar)

Abstract:

Generated Jacobian Equations have been introduced in 2014 by Trudinger as a generalization of Monge-Ampère equations arising in optimal transport. They were originally motivated by inverse problems arising in non-imaging optics, where the goal is to design optical components, such as mirrors or lenses, that transfer a given source light to a prescribed target light.In this talk, I will present a Newton algorithm for solving Generated Jacobian equations in the semi-discrete setting, meaning that one of the measures involved in the problem is finitely supported and the other one is absolutely continuous. Then I will apply it to the design of different kinds of mirrors or lenses that allow to transfer any punctual or collimated source to any target. This work is in collaboration with Anatole Gallouet and Quentin Mérigot.

Wednesday, 13 July 2022

Spectral theory of high-contrast random media

Matteo Capoferri (Prifysgol Caerdydd)

Abstract:

The talk is concerned with the rigorous mathematical description of propagation and localisation of waves in a particular class of composite materials with random microscopic geometry, called micro-resonant (or high-contrast) random media: small inclusions of a “soft” material are randomly dispersed in a “stiff” matrix. The highly contrasting physical properties of the two constituents, combined with a particular scaling of the inclusions, result in microscopic resonances, which manifest macroscopically by allowing propagation of waves in the material only within certain ranges of frequencies (band-gap spectrum).

High-contrast media with periodically distributed inclusions have been extensively studied and numerous results are available in the literature. However, their stochastic counterparts, which model more realistic scenarios and may exhibit localisation, are far from being well understood from a mathematical viewpoint. In my talk I will give an overview of existing results through the prism of stochastic homogenisation and spectral theory, and discuss recent advances and ongoing work.

Based on joint work with M. Cherdantsev and I. Velčić.

Monday, 8 August 2022

Vector valued extensions of operators through sparse domination and a multilinear UMD condition

Zoe Nieraeth (BCAM)

Abstract:

Vector-valued extensions of important operators in harmonic analysis have been actively studied in the past decades. A centerpoint of the theory is the result of Burkholder and Bourgain that the Hilbert transform extends to a bounded operator on L^p(R;X) if and only if the Banach space X has the so-called UMD property. In the specific case where X is a Banach function space, it is a deep result of Bourgain and Rubio de Francia that the UMD property is equivalent to the Hardy-Littlewood maximal operator having a bounded extension to both X and X’. In turn, this leads to powerful vector-valued extrapolation methods. In this talk I will place these ideas in the context of the more modern technique of domination by sparse forms. These forms are intimately related to Muckenhoupt weight classes and the multilsubinear Hardy-Littlewood maximal operator. Moreover, I will discuss some of work done in extending the UMD property to a multilinear setting. This talk is based on joint work with Emiel Lorist.

Wednesday, 10 August 2022

The Gregory–Laflamme Instability of the 5D Schwarzschild Black String Exterior

Sam Collingbourne (University of Cambridge)

Abstract: I will discuss a direct rigorous mathematical proof of the Gregory–Laflamme instability for the 5D Schwarzschild black string. This is a mode instability at the level of the linearised vacuum Einstein equation. Under a choice of ansatz for the perturbation and a gauge choice, the linearised vacuum Einstein equation can be reduced to a Schrödinger eigenvalue equation to which an energy functional is assigned. It is then shown by direct variational methods that the lowest eigenfunction gives rise to an exponentially growing mode solution which has admissible behaviour at the future event horizon and spacelike infinity in harmonic/transverse-traceless gauge.

Thursday 1st June 2023

Dualities on sets and how they appear in optimal transport

Katarzyna Wyczesany

Previous semesters (Virtual Maxwell Analysis Seminar)

Spring 2022

Friday, 21st January 2022

A dyadic approach to products of functions in 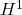$H^1$ and BMO

Odysseas Bakas (Basque Center for Applied Mathematics)

Abstract:

In 2011 Bonami, Grellier, and Ky proved that the product of a function in the Hardy space $H^1$ and a function of bounded mean oscillation can be written, in the sense of distributions, as a sum of an integrable function and an element in an appropriate Hardy-Orlicz space. Moreover, they showed that the decomposition operators can be taken to be bilinear.

In this talk we present a dyadic analogue of the result of Bonami, Grellier, and Ky and we show how their theorem can be recovered from its dyadic counterparts. Related topics in one and several parameters will also be discussed.

This is joint work Sandra Pott, Salvador Rodríguez-López, and Alan Sola.

Friday, 4th February 2022

Multijoints and Duality

Michael Tang (University of Edinburgh)

Abstract:

The multijoint problem is a discrete analogue to the multilinear Kakeya problem, and was solved by Zhang in 2016. More recently in 2020, Tidor, Yu and Zhao solved higher-dimensional generalisations of the multijoint problem. The multijoint and multilinear Kakeya problems can both be described by geometric multilinear inequalities for which there is a theory of duality, as established by Carbery, Hanninen and Valdimarsson. While the dual multilinear Kakeya problem is well understood, until now, the dual multijoint problem was not, despite the multijoint problem being solved by Zhang in 2016.

In this talk we formulate the multijoint problem as the boundedness of a multilinear operator and present a discrete analogue of a theorem due to Bourgain and Guth.

Friday, 11th February 2022

Diophantine Approximation as Cosmic Censor for AdS Black Holes

Christoph Kehle (Insitute for Advanced Study)

Abstract:

The statement that general relativity is a deterministic theory finds its mathematical formulation in the celebrated ‘Strong Cosmic Censorship Conjecture’ due to Roger Penrose. I will present my recent results on the linear analog of this conjecture in the case of negative cosmological constant. It turns out that this is intimately tied to Diophantine properties of a suitable ratio of mass and angular momentum of the black hole and that the validity of the conjecture depends in an unexpected way on the notion of genericity imposed.

Friday, 25th February 2022

Stability for geometric and functional inequalities

João Pedro Ramos (ETH Zürich)

Abstract:

The celebrated isoperimetric inequality states that, for a measurable set $S \subset \mathbb{R}^n,$ the inequality

$\text{per}(S) \ge n \text{vol}(S)^{\frac{n-1}{n}} \text{vol}(B_1)^{\frac{1}{n}}$

holds, where $\text{per}(S)$ denotes the perimeter (or surface area) of $S,$ and equality holds if and only if $S$ is an euclidean ball. This result has many applications throughout analysis, but an interesting feature is that it can be obtained as a corollary of a more general inequality, the Brunn–Minkowski theorem: if $A,B \subset \mathbb{R}^n,$ define $A+B = \{ a+b, a \in A, b\in B\}.$ Then

$|A+B|^{1/n} \ge |A|^{1/n} + |B|^{1/n}.$

Here, equality holds if and only if $A$ and $B$ are homothetic and convex. A question pertaining to both these results, that aims to exploit deeper features of the geometry behind them, is that of stability: if $S$ is close to being optimal for the isoperimetric inequality, can we say that $A$ is close to being a ball? Analogously, if $A,B$ are close to being optimal for Brunn–Minkowski, can we say they are close to being compact and convex?

These questions, as stand, have been answered only in very recent efforts by several mathematicians. In this talk, we shall outline these results, with focus on the following new result, obtained jointly with A. Figalli and K. Boroczky. If $f,g$ are two non-negative measurable functions on $\mathbb{R}^n,$ and $h:\mathbb{R}^n \to \mathbb{R}_{\ge 0}$ is measurable such that

$h(x+y) \ge f(2x)^{1/2} g(2y)^{1/2}, \, \forall x,y \in \mathbb{R}^n,$

then the Prekopa–Leindler inequality asserts that

$\int h \ge \left(\int f\right)^{1/2} \left( \int g\right)^{1/2},$

where equality holds if and only if $h$ is log-concave, and $f,g$ are `homothetic’ to $h$ , in a suitable sense. We prove that, if $\int h \le (1+\varepsilon) \left(\int f\right)^{1/2} \left( \int g\right)^{1/2},$ then $f,g,h$ are $\varepsilon^{\gamma_n}-$ $L^1-$ close to being optimal. We will discuss the general idea for the proof and, time-allowing, discuss on a conjectured sharper version.

Friday, 4th March 2022

Existence and uniqueness of solutions for the rotation-Camassa-Holm equation

Priscila Leal da Silva (Loughborough)

Abstract:

Since the discovery of the Camassa-Holm equation as an integrable peakon-equation, intense research has been dedicated to its generalisations of it and to the study of their solutions. Of particular interest in this talk is the rotation-Camassa-Holm equation (rCH), a nonlocally evolutive equation that takes into consideration the Coriolis force, which is typically a manifestation of rotation when Newton’s laws are applied to model physical phenomena on Earth’s surface. In this talk we present conditions for the existence of traveling wave solutions and show that, given an initial data in Sobolev spaces, uniqueness of local solutions is achieved. Moreover, assuming a strong condition on the McKean quantity, the solutions can be extended globally. Extensions of these results are presented, as well as further conjectures.

Friday, 11th March 2022

The elastic far-field development around a crystalline defect

Julian Braun (Heriot–Watt )

Abstract:

Lattice defects in crystalline materials (for example, a screw dislocations or an interstitial) create long-range elastic fields. In this presentation I will show how to rigorously derive a far-field expansion up to arbitrary high order. The expansion is computable and leaves only a fast decaying remainder describing the defect core structure. As an application I will also show how to use this expansion for high accuracy defect computations.

Friday, 18th March 2022

Zero-dispersion limit for the Benjamin-Ono equation on the torus

Louise Gassot (ICERM / University of Basel )

Abstract:

We discuss the zero-dispersion limit for the Benjamin-Ono equation on the torus given a single well initial data. We prove that there exist approximate initial data converging to the initial data, such that the corresponding solutions admit a weak limit as the dispersion parameter tends to zero. The weak limit is expressed in terms of the multivalued solution of the inviscid Burgers equation obtained by the method of characteristics. We construct our approximation by using the Birkhoff coordinates of the initial data, introduced by Gérard, Kappeler and Topalov.

Friday, 1st April 2022

Multi-material transport problems

Annalisa Massaccesi (Università di Padova)

Abstract:

Abstract: In this seminar I will review the theory of flat G-chains, as they were introduced by H. W. Fleming in 1966, and currents with coefficients in groups. One of the most recent developments of the theory concerns its application to the Steiner tree problem and other minimal network problems which are related with a Eulerian formulation of the branched optimal transport. Starting from a 2016 paper by A. Marchese and myself, I will show how these problems and their variants are equivalent to a mass-minimization problem in the framework of currents with coefficients in a (suitably chosen) normed group.

Autumn 2021

Friday, 1st October 2021

Mathematical aspects of nanophotonics

Matias Ruiz (University of Edinburgh)

Abstract:

In the last couple of decades, the field of nanophotonics, i.e. the study of light-matter interactions at the nanoscale, has gained enormous importance in different disciplines of science and engineering. A large portion of this field concerns the study of electromagnetic resonances in nanoparticles which are, in turn, the building blocks of many applications in energy, healthcare, material science, to name a few.

The description of these resonances relies on interesting math problems with strong connections to PDE spectral problems, both self-adjoint and non-self-adjoint. As such, there is a growing interest from the math world in tackling some of the mathematical issues arising in nanophotonics. For instance, a canonical problem is the Laplace transmission problem showing a sign-change in the PDE coefficients, whose solutions can be understood in terms of the spectral properties of the Neumann-Poincare operator (and/or the so-called plasmonic eigenvalue problem).

In this applied analysis talk I will introduce some of the mathematically interesting problems arising in nanophotonics and discuss recent analytical results in the analysis of resonances in metallic nanoparticles (also known as plasmonic resonances), which include the use of layer potential techniques and asymptotic analysis.

Friday, 8th October 2021

Harmonic analysis tools in spectral theory

Jean-Claude Cuenin (Loughborough University)

Abstract:

I will give a survey of how methods from harmonic analysis, particularly those related to Fourier restriction theory, can be used in spectral and scattering theory. Applications include eigenvalue estimates for Schrödinger operators with complex potentials and almost sure scattering for random lattice Schrödinger operators in 3d with slowly decaying potential.

Friday, 15th October 2021

Boundedness of spectral projectors on Riemannian manifolds

Simon Myerson (University of Warwick)

Abstract:

Given the Laplace(-Beltrami) operator on a Riemannian manifold, consider the spectral projector on (generalized) eigenfunctions whose eigenvalue lies in $[L^2,(L+\delta)^2]$ – where $L \gg 1$ and $\delta \ll 1$ . We ask the question of optimal $L^2$ to $L^p$ bounds for this operator. I will present new results in this direction for the Euclidean torus (joint with Pierre Germain).

Friday, 22nd October 2021

Multilinear Kakeya and Michael-Simon inequality for anisotropic stationary varifolds

Guido De Philippis (CIMS)

Abstract:

Michael Simon inequality is a fundamental tool in geometric analysis and geometric measure theory. Its extension to anisotropic integrands will allow to extend to anisotropic integrands a series of results which are currently known only for the area functional.

In this talk I will present an anistropic version of the Michael-Simon inequality, for for two-dimensional varifolds in $\mathbb{R}^3$ , provided that the integrand is close to the area in the C1-topology. The proof is deeply inspired by posthumous notes by Almgren, devoted to the same result. Although our arguments overlap with Almgren’s, some parts are greatly simplified and rely on a nonlinear version of the planar multilinear Kakeya inequality.

Friday, 29th October 2021

The equations of polyconvex thermoelasticity

Myrto Maria Galanopoulou (Heriot-Watt University)

Abstract:

In this talk, I will present the findings of my PhD Thesis. I will examine the system of thermoelasticity endowed with polyconvex energy. I will show that we can embed the equations of polyconvex thermoviscoelasticity into an augmented, symmetrizable, hyperbolic system which possesses a convex entropy. This allows to prove many important stability results, such as convergence from the viscous problem to smooth solutions of the system of adiabatic thermoelasticity in the zero-viscosity limit. In addition, I will present a weak-strong uniqueness result in the class of entropy weak solutions and in a suitable class of measure-valued solutions, defined by means of generalized Young measures. Also, we will discuss a variational scheme for isentropic processes of adiabatic polyconvex thermoelasticity: I establish existence of minimizers which converge to a measure-valued solution that dissipates the total energy, while the scheme converges when the limiting solution is smooth.

Friday, 5th November 2021

Energy transfer for solutions to the nonlinear Schrodinger equation on irrational tori.

Gigliola Staffilani (MIT)

Abstract:

In this talk I will outline some results on the study of transfer of energy for solutions to the periodic 2D (torus domain) cubic defocusing nonlinear Schrodinger equation. In particular I will focus on the differences of the dynamics of solutions in the rational versus irrational torus. Some numerical experiments will also be presented.

(The most recent work presented is in collaboration with A. Hrabski, Y. Pan and B. Wilson.)

Friday, 19th November 2021

Dynamical fluctuations of a hard sphere gas in the low density limit

Laure Saint-Raymond (IHES)

Abstract:

The dynamics of a hard sphere gas is described in the low density limit by the Boltzmann equation, at least for short times. The classical strategy of proof, due to Lanford, fails for longer times, even close to equilibrium.In this talk, I will present a recent work with T. Bodineau, I. Gallagher and S. Simonella, where we have designed a new method, combining a duality and a pruning arguments, which allows to characterize the fluctuations around equilibrium globally in time.

Friday, 26th November 2021

Polynomial progressions in continuous fields

Jim Wright (University of Edinburgh)

Abstract:

In 1988 Bourgain gave a quantitative count for the number of progressions $x, x+t, x+t^2$ in dense sets on the real line. Recently this was extended to general 3-term polynomial progressions by X. Chen, J. Guo and X. Li. In this talk we extend these results to arbitrarily long polynomial progressions. Our methods are robust enough

to give quantitative counts for long polynomial progressions in any locally compact topological field with nontrivial topology. This is joint work with B. Krause, M. Mirek and S. Peluse.

Friday, 10th December 2021

On the strong cosmic censorship conjecture

Jan Sbierski (University of Edinburgh)

Abstract:

The strong cosmic censorship conjecture roughly states that Einstein’s theory of general relativity is generically a deterministic theory. I will start out this talk by giving a non-technical introduction to this conjecture restricted to rotating black holes. After motivating the mathematical formulation of the strong cosmic censorship conjecture I will proceed to outline the current state of it and then conclude by presenting forthcoming work of mine showing the linear instability of the Cauchy horizon inside rotating black holes.

Spring 2021

Friday, 22nd January 2021

Topological properties of minimizers in Landau-de Gennes theory of nematic liquid crystals

Federico Luigi Dipasquale (Università di Verona)

Abstract:

I will talk about recent results on the topology of minimizers in the Landaude Gennes (LdG) theory of nematic liquid crystals which shed light on the socalled “biaxial torus minimizers”. According to many numerical studies, these are the minimizers of the most studied LdG energy in very relevant physical conditions. Such minimizers are axially symmetric and characterized by remarkable topological properties (where the topology is to be sought in the level set of an appropriate indicator function, the signed biaxiality). However, they eluded precise mathematical description for years. In this talk, I will introduce some new key ideas which allow to study the topology of minimizers (but also of some classes of more general configurations). I will try to explain how to implement them and how this leads in a natural way to the definition of an appropriate asymptotic regime in which, in fact, topological structures are found in the biaxiality sets of minimizers. The topological results match qualitatively many features expected from the numerical simulations. We will also see that, restricting to axially symmetric configurations, we have still better accordance with simulations and much more can be said, although several interesting problems remain open. Joint work with V. Millot (Paris XIII) and A. Pisante (Sapienza).

Friday, 29th January 2021

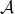$\mathcal{A}$ -quasiconvexity, function spaces and regularity

Franz Gmeineder (Universität Bonn)

Abstract:

By Morrey’s foundational work, quasiconvexity displays a key notion in the vectorial Calculus of Variations. A suitable generalisation that keeps track of more elaborate differential conditions is given by Fonseca & Müller’s $\mathcal{A}$ -quasiconvexity. With the topic having faced numerous contributions as to lower semicontinuity, in this talk I give an overview of recent results for such problems with focus on the underlying function spaces and the (partial) regularity of minima. The talk is partially based on joint work with Sergio Conti (Bonn), Jan Kristensen (Oxford) and Lars Diening (Bielefeld).

Friday, 5th February 2021

Landis’ conjecture on the decay of solutions to Schrödinger equations on the plane

Eugenia Malinnikova (Stanford)

Abstract:

We consider a real-valued function on the plane for which the absolute value of the Laplacian is bounded by the absolute value of the function at each point. In other words, we look at solutions of the stationary Schrödinger equation with a bounded potential. The question discussed in the talk is how fast such function may decay at infinity. We give the answer in dimension two, in higher dimensions the corresponding problem is open. The talk is based on the joint work with A. Logunov, N. Nadirashvili, and F. Nazarov.

Friday, 12th February 2021

Global invertibility via invertibility on boundary and applications to Nonlinear Elasticity

Stefan Krömer (Czech Academy of Sciences)

Abstract:

Globally invertible Sobolev maps are of particular interest in models for the elastic deformation of solids, because invertibility corresponds to non-interpenetration of matter. By a result of John Ball (1981), a locally orientation preserving Sobolev map is almost everywhere globally invertible provided that its boundary values admit a homeomorphic extension. We will see that the conclusions of Ball’s theorem and related results can be reached while completely avoiding the (hard) problem of homeomorphic extension. The proof heavily relies on Brouwer’s topological degree. Among other things, the result can be applied to justify more efficient numerical approximation respecting global invertibility constraints.

Friday, 19th February 2021

The nonlinear stability of the Schwarzschild black hole without symmetry

Mihalis Dafermos (Cambridge/Princeton)

Friday, 26th February 2021

Hölder continuous Euler flows with local energy dissipation

Hyunju Kwon (IAS)

Abstract:

The Euler equations describe the behavior of ideal fluids. It is well-known that smooth (spatially periodic) Euler flows conserve total kinetic energy in time. In the theory of turbulence, on the other hand, a famous conjecture of Lars Onsager asserts that kinetic energy conservation may fail when an Euler flow belongs to the Hölder spaces with Hölder exponent less than 1/3, which was proved recently by Isett. In light of these developments, I’ll discuss a stronger version of the Onsager conjecture: the existence of Hölder continuous Euler flows which locally dissipate kinetic energy.

Friday, 5th March 2021

Regularity of solutions of complex coefficient elliptic systems: the 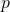$p$ -ellipticity condition

Jill Pipher (Brown)

Abstract:

Formulating and solving boundary value problems for divergence form real elliptic equations has been an active and productive area of research ever since the foundational work of De Giorgi – Nash – Moser established H\”older continuity of solutions when the operator coefficients are merely bounded and measurable. The solutions to such real-valued equations share some important properties with harmonic functions: maximum principles, Harnack principles, and estimates up to the boundary that enable one to solve Dirichlet problems in the classical sense of nontangential convergence. Weak solutions of complex elliptic equations and elliptic systems do not necessarily share these good properties of continuity or maximum principles. In joint work with M. Dindos, we introduced in 2017 a structural condition ( $p$ -ellipticity) on divergence form complex elliptic equations that was inspired by a condition related to $L^p$ contractivity due to Cialdea and Maz’ya. The $p$ -ellipticity condition was also simultaneously discovered by Carbonaro-Dragicevic, who used it to prove a bilinear embedding result. Subsequently, the condition has proven useful in the study of well-posedness of a degenerate elliptic operator associated with domains with lower-dimensional boundary. In this talk we discuss $p$ -ellipticity for complex divergence form equations, and then describe recent work, joint with J. Li and M. Dindos, extending this condition to elliptic systems. In particular, we give applications to solvability of the Dirichlet problem for the Lame systems.

Friday, 12th March 2021

Rigidity for measurable sets

Ilaria Fragalé (Politecnico di Milano)

Abstract:

We discuss the rigidity of measurable subsets in the Euclidean space such that the Lebesgue measure of their intersection with a ball of radius $r$ , centred at any point in the essential boundary, is constant. Based on a joint work with Dorin Bucur.

Friday, 19th March 2021

A 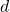$d$ -dimensional Analyst’s Travelling Salesman Theorem for general sets in Euclidean space

Matthew Hyde (University of Edinburgh)

Abstract:

In the nineties, Peter Jones proved the Analyst’s Travelling Salesman Theorem (TST), which gives a necessary and sufficient condition for when a set in Euclidean space can be contained in a curve of finite length. This condition is stated in terms of beta-numbers, which give a measure of how flat a set is at each location and scale. Several higher dimensional analogues of the TST have been proven since. These, along with Jones’ original result, have found many applications in fields such as complex analysis, harmonic analysis, and harmonic measure. Unlike Jones’ TST, these higher dimensional variants require additional assumption on the set. In this talk we will discuss these results in more detail and introduce a higher dimensional TST that holds for every set in Euclidean space.

Friday, 26th March 2021

Discrete analogues of maximally modulated singular integrals of Stein-Wainger type

Joris Roos (University of Massachusetts Lowell & University of Edinburgh)

Abstract:

Stein and Wainger introduced an interesting class of maximal oscillatory integral operators related to Carleson’s theorem. The talk will be about joint work with Ben Krause on discrete analogues of some of these operators. These discrete analogues feature a number of substantial difficulties that are absent in the real-variable setting and involve themes from number theory and analysis.

Comments are closed

Comments to this thread have been closed by the post author or by an administrator.

Toggle navigation menu Menu

Analysis seminar

Regularity for semilinear variational problems with a topological constraint

Anna Skorobogatova (ETH Zürich)

Spring 2025

Regularity for semilinear variational problems with a topological constraint

Anna Skorobogatova (ETH Zürich)

Sharp spectral projection estimates for the torus

Daniel Pezzi (Johns Hopkins)

Maxwell Analysis Mini-symposium

1:00pm Pierre Germain (Imperial College)

Asymptotic stability of solitary waves in nonlinear dispersive equations

2:30pm Laure Saint-Raymond (IHES)

The effect of viscosity on internal waves

Pathwise local well-posedness of stochastic nonlinear wave equations with multiplicative noises

Jiawei Li (University of Edinburgh)

A problem in quasilinear wave equations

Pieter Blue & Jan Sbierski (University of Edinburgh)

Convex sets can have interior hot spots

Juame de Dios Pont (ETH Zürich)

Three discrete maximal functions in high dimensions – Gaussians, balls and spheres

Błażej Wróbel (University of Wrocław)

Hyperbolic nonlinear Schrödinger equations

Yuzhao Wang (University of Birmingham)

Regularity of maximal functions

Julian Weigt (University of Warwick)

Symmetric low-regularity integrators for dispersive nonlinear equations

Georg Maierhofer (University of Cambridge)

On some Thomas-Fermi type variational problems

Damiano Greco (University of Edinburgh)

Autumn 2024

Maxwell Analysis Mini-Symposium

The dimension of random subsets of Cantor sets defined by trees of coin flips

Lauritz Streck (University of Edinburgh)

Pointwise localization and sharp weighted bounds for Rubio de Francia square functions

Mikel Florez (BCAM)

Dimension interpolation and exceptional set estimates

Ana Emilia de Orellana (St. Andrews)

Fourier multipliers on SL(2,Z) and SL(2,R)

Sharp Fourier restriction over finite fields

Cristian González-Riquelme (Instituto Superior Tecnico in Lisbon)

Uniform Boundedness for Linearised Gravity on Schwarzschild from the Canonical Energy

Sam Collingbourne (University of Edinburgh)

Scottish-Basque Analysis meeting

An intersection of CS and harmonic analysis: approximating matrix p to q norms

Dominique Maldague (University of Cambridge)

Counting Rational Points near Smooth Manifolds

Rajula Srivastava (University of Bonn and the Max Planck Institute for Mathematics)

Stability and instability of extremal black holes

Dejan Gajic (Leipzig University)

Maxwell Analysis Mini-Symposium

Summer 2024

Multilinear and Weighted Estimates for Oscillatory Integral Operators

David Rule (Linköping University)

Some Developments in the Eigenvalue Distribution of Spatio-Spectral Limiting Operators in two domains

Azita Mayeli (City University of New York)

Spring 2024

Variable coefficient Lp local smoothing and applications

Future stability of spatially homogeneous Friedmann–Lemaitre–Robertson–Walker solutions of the Einstein–massless Vlasov system

Rectifiability and tangents in a rough Riemannian setting

Deep-water and shallow-water limits of statistical equilibria for the intermediate long wave equation

Elliptic PDE with Hölder data in rough sets

Stochastic compactness method and the Camassa–Holm equation with gradient noise

Global stability of Kaluza-Klein spacetimes

Sharp quasi-invariance threshold for the cubic Szeg\H{o} equation

James Coe (UoE)

Maxwell Analysis Mini-Symposium

Grigori Rozenbloum (Chalmers University of Technology, Sweden)

Title: Weyl asymptotics for eigenvalues of Poincare-Steklov problem in a domain with Lipschitz boundary

Susanna Terracini (University of Turin, Italy)

Title: Rotating Spirals in competition-difuision systems

Eugene Shargorodsky (King’s College London)

Title: Variations on Liouville’s theorem

90 years of pointwise ergodic theory

Ben Krause (University of Bristol)

The Dirac equation in dispersive PDEs: advances and open problems

T1 theorem: boundedness and compactness of Calderón-Zygmund operators

Previous semester

Autumn 2023

Disproving the Deift conjecture: the loss of almost periodicity

The Euclidean $\Phi^4_2$ theory as the limit of an interacting Bose gas

Heat flow regularisation, Brascamp—Lieb inequality, and convex
geometry

Solvability of the Poisson problem with interior data in $L^p$ Carleson spaces and its applications to the regularity problem.