Past Seminars and Recordings

Friday, April 4, 2025

Chengcheng Ling (University of Augsburg)

Title: Regularization by multiplicative noise

Abstract:

Regularization by noise in the context of stochastic differential equations (SDEs) with coefficients of low regularity, known as singular SDEs, refers to the beneficial effect produced by noise so that the singularity from the coefficients is smoothed out yielding well-behaved equations. This field, initiated by works of Zvonkin and Veretennikov from 70’s, has been extensively explored among different concepts from stochastic calculus. In this talk we will introduce the ideas from classical Itô calculus, involving partial differential equation (PDE) theory and modern tools from rough path theory and Malliavin calculus, to address problems related to the well-posedness and numerics of singular SDEs driven by different types of noise, particularly multiplicative Gaussian noise.

Tuesday, April 1, 2025

Giuseppe Cannizzaro (University of Warwick)

Title: Superdiffusive Central Limit Theorem for the Stochastic Burgers Equation at the critical dimension

Abstract:

The Stochastic Burgers Equation (SBE) was introduced in the eighties by van Beijren, Kutner and Spohn as a mesoscopic model for driven diffusive systems with one conserved quantity. In the subcritical dimension d=1, it coincides with the derivative of the KPZ equation whose large-scale behaviour is polynomially superdiffusive and given by the KPZ Fixed Point, and in the super-critical dimensions d>2, it was recently shown to be diffusive and rescale to an anisotropic Stochastic Heat equation. At the critical dimension d=2, the SBE was conjectured to be logarithmically superdiffusive with a precise exponent but this has only been shown up to lower order corrections. This talk is based on the work joint with Fabio Toninelli and Quentin Moulard under the same name https://arxiv.org/abs/2501.00344, where we pin down the logarithmic superdiffusivity by identifying exactly the large-time asymptotic behaviour of the so-called diffusion matrix and show that, once the logarithmic corrections to the scaling are taken into account, the solution of the SBE satisfies a central limit theorem. This is the first superdiffisive scaling limit result for a critical SPDE, beyond the weak coupling regime.

Recording: https://ed-ac-uk.zoom.us/rec/share/D-OFJLfRXiO2rN-we2Bc-oiT6764RfNfNPz6LBy-gIbUHhqpYfGav8CibSyEildW.6c_l23pYy_NaT1_Q?startTime=1743512687000

Tuesday, March 25, 2025 [Online]

Mitia Duerinckx (Université Libre de Bruxelles)

Title: A duality method for mean-field limits with singular interactions

Abstract:

One major open problem in mathematical physics still concerns the justification of the Vlasov-Poisson equation as the mean-field limit for systems of classical particles with Coulomb interactions. In this talk, we present a new approach to the problem, based on a duality argument combined with a hierarchical analysis of dual linear correlations. Although it does not allow to justify Vlasov-Poisson even in 2D, it allows us to cover for the first time arbitrary square-integrable interaction forces at possibly vanishing temperature, and it further yields nontrivial convergence rates. Joint work with Didier Bresch and Pierre-Emmanuel Jabin.

Recording: https://ed-ac-uk.zoom.us/rec/share/T_z173X4fXCmr-ts3MeA2bOFguz5alFx45L2389rvNY7W1sGdRmgXUyuFB8hTW5x.UV3L9yflUoM0MGcP?startTime=1742911529000

Tuesday, March 18, 2025 [Online]

Travis Scrimshaw (Hokkaido University)

Title: TASEP and Schubert Kalculus

Abstract:

In 2008, Dieker and Warren computed the n-step transition probabilities of 4 different versions of discrete time TASEP on the line with time and particle inhomogeneities and with the step initial condition. In this talk, we reinterpret these transitions in terms of symmetric functions that arise from a seemingly unconnected area: K-theoretic Schubert calculus of the Grassmannian. We do so by describing the relationship using the boson-fermion correspondence from mathematical physics, which forms the basis of the Okounkov-Reshetikhin method of computing the correlation kernel of the Schur process. We conclude with a generalization to a position inhomogeneous process, but that behaves in a more “bosonic” way. This is based on joint work with Shinsuke Iwao and Kohei Motegi (arXiv: 2311.01116).

Wednesday, March 19, 2025

Ruoyuan Liu (University of Bonn)

Title: Global dynamics and weak universality for the fractional hyperbolic 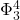$\Phi^4_3$ -model

Abstract:

In this talk, I consider the 3-dimensional stochastic damped fractional nonlinear wave equation (with order $\alpha > 1$ ) with a cubic nonlinearity, also known as the fractional hyperbolic $\Phi^4_3$ -model. The construction of the fractional $\Phi^4_3$ -measure (Gibbs measure for the fractional hyperbolic $\Phi^4_3$ -model) exhibits a phase transition: when $\alpha > 9/8$ , the Gibbs measure is equivalent with the base Gaussian measure; when $1 < \alpha \leq 9/8$ , the Gibbs measure is mutually singular with the base Gaussian measure. I will first talk about global well-posedness of the fractional hyperbolic $\Phi^4_3$ -model and invariance of the fractional $\Phi^4_3$ -measure for the entire range $\alpha > 1$ . Then, I will discuss weak universality for the fractional hyperbolic $\Phi^4_3$ -model. In the case $\alpha > 9/8$ , we prove weak universality by using a first order expansion, invariance of Gibbs measures, and space-time analysis. In the case $1 < \alpha <= 9/8$ , we also obtain weak universality by overcoming the issue of singularity between the Gibbs measure and the base Gaussian measure.Some parts of the talk are based on a joint work with Nikolay Tzvetkov (ENS Lyon) and Yuzhao Wang (University of Birmingham).

Tuesday, March 11, 2025 [Online]

Jiaoyang Huang (University of Pennsylvania)

Title: Ramanujan Property and Edge Universality of Random Regular Graphs

Abstract:

Extremal eigenvalues of graphs are of particular interest in theoretical computer science and combinatorics. Specifically, the spectral gap—the difference between the largest and second-largest eigenvalues—measures the expansion properties of a graph. In this talk, I will focus on random d-regulargraphs.

I will begin by providing background on the eigenvalues of random d-regulargraphs and their connections to random matrix theory. In the second part of the talk, I will discuss our recent results on eigenvalue rigidity and edge universality for these graphs. Eigenvalue rigidity asserts that, with high probability, each eigenvalue concentrates around its classical location as predicted by the Kesten-McKay distribution. Edge universality states that the second-largest eigenvalue and the smallest eigenvalue of random d-regulargraphs converge to the Tracy-Widom distribution from the Gaussian Orthogonal Ensemble. Consequently, approximately 69% of d-regular graphs are Ramanujan graphs. This work is based on joint work with Theo McKenzie and Horng-Tzer Yau.

Recording: https://ed-ac-uk.zoom.us/rec/share/WxEWcsngLuLHQnlbjidV1YwcwtZW51Y1hKabTSkRLEl9Z9Hej-r2rd0gsW3g1Do.5WG2bvSSzXE90ioW

Tuesday, March 4, 2025

Nicos Georgiou (University of Sussex)

Title: The tree-TASEP on Galton-Watson trees

Abstract:

We define a totally asymmetric simple exclusion process on trees, where the particles enter the tree from a reservoir attached to the root.

Particles can only jump following edges on the tree and only if they are jumping away from the root, to a non-occupied vertex.

We are interested in two different aspects of this particle system. First we want to investigate the current of particles across a given generation at a specific time, when we start from an initially empty initial condition. Second, we would like to obtain some information about the current across a given ray. Both answers depend heavily on our choice of jump rates for the particles and the tree geometry and different regimes of behaviour will be presented during the talk. Our results rely on a crucial estimate of the time it takes for the trajectories of the first N particles to decouple in the tree.

This is joint work with N. Gantert (TUM) and D. Schmid (Columbia).

Tim Johnston (Université Paris Dauphine)

Title: Privacy Guarantees for Stochastic Processes

Abstract:

In this talk we shall discuss differential privacy, a framework for quantifying the extent to which a random output depends on the information used to produce it. After introducing several related definition of differential privacy, we shall discuss techniques used to show the differential privacy of both trajectories and single draws from stochastic processes. In doing so we shall touch on a recent perturbation technique which allows for Wasserstein type bounds to be converted into stronger distances like the KL and Renyi divergence.

Recording: https://ed-ac-uk.zoom.us/rec/share/WCdvckBo_CNthIopGI1ryd-sxYRrk3EySguNu0ww13vcTQJ_uj-HTF0LPrExmyFU.G1qnbuBdfxDyM6h-?startTime=1741097194000

Tuesday, February 25, 2025 [Online]

Sung-soo Byun (Seoul National University)

Title: Spectral moments and Harer–Zagier type recursion formulas in random matrix theory

Abstract: Random matrix theory enjoys an intimate connection with various branches of mathematics. One prominent illustration of this relationship is the Harer–Zagier formula for spectral moments, which serves as a well-known example demonstrating the combinatorial and topological significance inherent in random matrix statistics. While the Harer–Zagier formula originates from the study of the moduli space of curves, it also gives rise to a fundamental formula in the study of spectral moments of classical random matrices. In this talk, I will introduce Harer–Zagier type formulas for classical Hermitian Gaussian random matrix ensembles and present recent progress across various models.

recording: https://ed-ac-uk.zoom.us/rec/share/SyaiaALOrBYMhZTG5wc_QS7_j8ltQC4hmISjV3POvmieMpxq5L2UAtAAbFSAP0Q.CcztJ5wrNd6ScdNr

Tuesday, February 4, 2025

George Yin (University of Connecticut)

Title: Deep Filtering

Abstract:

Nonlinear filtering is a fundamental problem in signal processing, information theory, communication, control and optimization, and systems theory. In the 1960s, celebrated results on nonlinear filtering were established. Nevertheless, the computational issues for nonlinear filtering remained to be a long-standing (60-year-old) and challenging problem. In this talk, instead of working with stochastic partial differential equations for obtaining the conditional distribution, we construct finite-dimensional approximations using deep neural networks for the optimal weights. Two recursions are constructed in the algorithm. One of them is the approximation of the optimal weight and the other is for approximating the optimal learning rate. [This is a joint work with Hongjiang Qian (Auburn University) and Qing Zhang (University of Georgia).]

Tuesday, January 28, 2025 [Online]

Giorgio Cipolloni (University of Arizona)

Title: Logarithmically correlated fields from non-Hermitian random matrices

Abstract:

We study the Brownian evolution of large non-Hermitian matrices and show that their log-determinant converges to a 2+1 dimensional Gaussian field in the Edwards-Wilkinson regularity class, i.e. logarithmically correlated for the parabolic distance. This gives a dynamical extension of the celebrated result by Rider and Virag (2006) proving that the fluctuations of the eigenvalues of Gaussian non-Hermitian matrices converge to a 2 dimensional log-correlated field. Our result, previously not known even in the Gaussian case, holds out of equilibrium for general matrices with i.i.d. entries.

We also study the extremal values of these fields and demonstrate their logarithmic dependence on the matrix dimension.

Recording:

https://ed-ac-uk.zoom.us/rec/share/x-hVTP7rwXQDNxM7KYQSpXk9gxzOuAxan_dBGaCOQ6WnG3OLFo-GNLUGUDy2fQAk.RUa7wTuK9eMLatii

Tuesday, January 21, 2025 [In Person Only]

Philippe Sosoe (Cornell University)

Title: The incipient infinite cluster in high dimensional percolation: a robust construction

Abstract:

Bernoulli percolation is one of the simplest models of statistical mechanics which exhibits a second order phase transition: it is expected that at the exact critical density above which there is almost surely an infinite cluster on the lattice, the cluster of the origin is almost surely finite, but its expected size is infinite. This raises the question of whether a critical percolation process with the cluster of the origin conditioned to be infinite can be defined.

Such a process was constructed in dimension 2 by Kesten, and in various versions in sufficiently high dimensions by van der Hofstad-Jarai and later Heydenreich-van der Hofstad-Hulshof. These constructions use a diagrammatic expansion called the lace expansion, and are partially conditional.

In this talk, I will explain a new construction of the IIC which circumvents the need for the lace expansion and gives an unconditional result.

Joint work with P Chinmay, J Hanson and S Chatterjee.

Tuesday, December 3, 2024 [Jointly with Analysis Seminar at UoE]

Zhenjie Ren (University Evry Paris-Saclay)

Title: Self-interacting approximation to McKean-Vlasov long time limit

Abstract:

Motivated by the mean-field optimization model of the training of two-layer neural networks, we propose a novel method to approximate the invariant measures of a class of McKean-Vlasov diffusions. We introduce a proxy process that substitutes the mean-field interaction with self-interaction through a weighted occupation measure of the particle’s past. If the McKean-Vlasov diffusion is the gradient flow of a convex mean-field potential functional, we show that the self-interacting process exponentially converges towards its unique invariant measure close to that of the McKean-Vlasov diffusion. As an application, we show how to learn the optimal weights of a two-layer neural network by training a single neuron.

Sergey Bobkov (University of Minnesota)

Title: Refinements of Berry-Esseen inequality in terms of Lyapunov coefficients

Abstract:

We discuss some variants of the Berry–Esseen inequality in terms of Lyapunov coefficients which may provide sharp rates of normal approximation.

Tuesday, November 26, 2024

Lingfu Zhang (Caltech)

Title: Airyβ line ensemble

Abstract:

In the past decades, a family of distributions, indexed by a parameter β and named after Tracy-Widom, have been found in a wide range of correlated random systems: first in random matrices (β=1,2,4), then random permutations, interacting particle systems, growth processes, and many others. The β=2 Tracy-Widom distribution has been extended to a random process called Airy line ensemble, which has been proven to be the limit of, e.g., interfaces from the KPZ universality class. For any other β>0, such an extension has been expected, while much less is known, due to the absence of many structures special for β=2. In this talk, I will report our recent progress, in two perspectives: we construct the Airyβ line ensemble through exact formulas, and we characterize it using an SDE, thereby providing a general framework of proving convergence. This is based on a joint work with Vadim Gorin and Jiaming Xu, and a joint work with Jiaoyang Huang.

Tuesday, November 19, 2024

Tom Klose (University of Oxford)

Title: Large deviations for the Φ^4_3 measure via Stochastic Quantisation

Abstract:

The Φ^4_3 measure is one of the easiest non-trivial examples of a Euclidean quantum field theory (EQFT) whose rigorous construction in the 1970’s has been one of the celebrated achievements of the Constructive QFT community. In recent years, progress in the field of singular stochastic PDEs, initiated by the theory of regularity structures, has allowed for a new construction of the Φ^4_3 EQFT as the invariant measure of a previously ill-posed Langevin dynamics – a strategy originally proposed by Parisi and Wu (’81) under the name Stochastic Quantisation. In this talk, I will demonstrate that the same idea also allows to transfer the large deviation principle for the Φ^4_3 dynamics, obtained by Hairer and Weber (’15), to the corresponding EQFT. Our strategy is inspired by earlier works of Sowers (’92) and Cerrai and Röckner (’05) for non-singular dynamics and potentially also applies to other EQFT measures. This is joint work with Avi Mayorcas (University of Bath), see arXiv:2402.00975. If time permits, I will briefly explain how similar techniques may be used to study exit problems for the 3D Stochastic Allen–Cahn equation which is a joint work in progress with Ioannis Gasteratos (TU Berlin).

Recording: https://ed-ac-uk.zoom.us/rec/share/HK5py_a14qmnKmlMao_rdUjRFFRlceE-DieJhjWJl-8fJK_LZCZG5NTZ9rR5D-Mb.xUvFNc9Hlk0tVTTj?startTime=1732025347000

Roxana Dumitrescu (King’s College London)

Title: A new Mertens decomposition of Y g,ξ-submartingale systems and applications

Abstract:

We introduce the concept of Y g,ξ-submartingale systems, where the nonlinear operator Y g,ξ corresponds to the first component of the solution of a reflected BSDE with generator g and lower obstacle ξ. We first show that, in the case of a left-limited right-continuous obstacle, any Y g,ξ-submartingale system can be aggregated by a process which is right-lower semicontinuous. We then prove a Mertens decomposition, by using an original approach which does not make use of the standard penalization technique. These results are in particular useful for the treatment of control/stopping game problems and, to the best of our knowledge, they are completely new in the literature. We finally present two applications in Finance.

Verena Schwarz (University of Klagenfurt)

Title: Milstein scheme for McKean–Vlasov SDEs driven by Brownian motion and Poisson random measure

Abstract:

In this talk we study the numerical approximation of the McKean–Vlasov SDEs driven by Brownian motion and Poisson random measure with super-linearly growing drift, diffusion and jump-coefficient. In a first step we derive the corresponding interacting particle system and define a Milstein-type approximation for this. Making use of the propagation of chaos result and investigating the error of the Milstein-type scheme we provide convergence results for the scheme. In a second step we discuss potential simplifications of the numerical approximation scheme for the direct approximation of the McKean–Vlasov SDE. Lastly, we present the results of our numerical simulations.

Tuesday, November 12, 2024

Amanda Turner (University of Leeds)

Title: Growth of Stationary Hasting-Levitov

Abstract:

Planar random growth processes occur widely in the physical world. One of the most well-known, yet notoriously difficult, examples is diffusion-limited aggregation (DLA) which models mineral deposition. This process is usually initiated from a cluster containing a single “seed” particle, which successive particles then attach themselves to. However, physicists have also studied DLA seeded on a line segment. One approach to mathematically modelling planar random growth seeded from a single particle is to take the seed particle to be the unit disk and to represent the randomly growing clusters as compositions of conformal mappings of the exterior unit disk. In 1998, Hastings and Levitov proposed a family of models using this approach, which includes a version of DLA. In this talk I will define a stationary version of the Hastings-Levitov model by composing conformal mappings in the upper half-plane. This is proposed as a candidate for off-lattice DLA seeded on the line. We analytically derive various properties of this model and show that they agree with numerical experiments for DLA in the physics literature.

Tuesday, November 5, 2024

Thomas Leblé (Université de Paris-Cité)

Title: Some recent progress on the 2DOCP

Abstract:

The two-dimensional one-component “plasma” or “Coulomb gas” is an important model of statistical physics, which has a close connection with eigenvalues of random matrices, with zeroes of Gaussian analytic functions, and with determinantal point processes.
I will give an overview of some recent results showing a strong form of “order” among this system at all temperatures: hyperuniformity, number-rigidity, translation-invariance… some of which were predicted long ago in the physics literature.
Figuring out its phase portrait remains nonetheless an open question.

Tuesday, October 22, 2024

Guopeng Li (Beijing Institute of Technology)

Title: Nonlinear PDEs with modulated dispersion – regularization by noise

Abstract:

We study dispersive equations with a time non-homogeneous modulation acting on the linear dispersion term. In this talk, we consider the Korteweg-de Vries equation (KdV) and related equations such as the Benjamin-Ono equation (BO) and the intermediate long wave equation (ILW). By imposing irregularity conditions on the modulation, we demonstrate phenomena known as regularization by noise in the following three ways:

(i) For sufficiently irregular modulation, we establish local well-posedness of the modulated KdV on both the circle and real line in settings where the unmodulated KdV is ill-posed. In particular, we show that the modulated KdV on the circle with a sufficiently irregular modulation is locally well-posed in Sobolev spaces of arbitrarily low regularity. By combining the $I$ -method (from dispersive PDEs) and the sewing lemma (controlled rough paths), we also prove global well-posedness in negative Sobolev spaces.

(ii) While equations like BO and ILW exhibit quasilinear behavior, we show that sufficiently irregular modulations semilinearize these equations by proving their local well-posedness via a contraction argument.

(iii) Finally, we show nonlinear smoothing for these modulated equations, where we show that a gain of regularity of the nonlinear part becomes (arbitrarily) larger for more irregular modulations.

This talk is based on joint work with Khalil Chouk (formerly UoE), Massimiliano Gubinelli (Oxford), Tadahiro Oh (UoE), and Jiawei Li (UoE).

Tuesday, October 15, 2024

Darrick Lee (University of Edinburgh)

Title: Towards Rough Surfaces

Abstract:

The path signature is a rich description of paths which plays a fundamental role in the theory of rough paths. The expected signature allows us to characterize the law of (possibly highly irregular) stochastic processes, providing a notion of moments for path-valued probability measures. Path signatures satisfy a fundamental property that it preserves the concatenation structure of paths. In this talk, we discuss a generalization of the path signatures to surfaces, which preserves the higher algebraic structure of horizontal and vertical concatenations. Furthermore, we discuss how this surface signature can be computed for highly irregular (rough) surfaces.

Tuesday, October 1, 2024

Joseph Najnudel (University of Bristol)

Title: Circular ensembles, orthogonal polynomials and Gaussian multiplicative chaos

Abstract:

We present strong connections between the Circular Beta Ensemble and the Gaussian multiplicative chaos, which is a random measure constructed by exponentiating a logarithmically correlated field. These connections are established by using the theory of orthogonal polynomials on the unit circle. In particular, in the subcritical and the critical phase, we identify the joint distribution of the Verblunky coefficients of the recursion satisfied by the orthogonal polynomials associated to the Gaussian multiplicative chaos, showing that these Verblunsky are directly connected to the Circular Beta Ensemble via a construction by Killip and Nenciu.

Zahra Sadat Mirsajjadi (University of Edinburgh)

Title: Infinite-dimensional diffusions from random matrix dynamics

Abstract:

I will talk about the infinite particle limit of eigenvalue stochastic dynamics introduced by Rider and Valko. These are the canonical dynamics associated to the inverse Laguerre ensemble in the way Dyson Brownian motion is related to the Gaussian ensemble. For this model we can prove convergence, from all initial conditions, to a new infinite-dimensional Feller process, describe the limiting dynamics in terms of an infinite system of log-interacting SDE that is out-of-equilibrium and finally show convergence in the long-time limit to the equilibrium state given by the (inverse points of the) Bessel determinantal point process.

Tuesday, September 24, 2024

Mathieu Laurière (Online, NYU Shanghai)

Title: Reinforcement learning for mean field games and mean field control problems

Abstract:

Mean field games have been introduced to study Nash equilibria in large populations of strategic agents, while mean field control problems aim at modeling social optima in large groups of cooperative agents. These frameworks have found a wide range of applications, from economics and finance to social sciences and biology. In the past few years, the question of learning equilibria and social optima in a mean field setting has attracted a growing interest. In this talk, we will discuss several model-free methods based on reinforcement learning. We will in particular introduce the notion of mean field Markov decision processes to tackle discrete time mean field control problems with common noise. Numerical experiments on stylized examples will be presented.

Thursday, July 4, 2024

Matteo Mucciconi (University of Warwick)

Title: Large Deviations for the height function of the deformed polynuclear growth.

Abstract:

The deformed polynuclear growth is a growth process that generalizes the polynuclear growth studied in the context of KPZ universality class. In this talk, I will discuss the mathematical derivation of large time large deviations for the height function. Rare events, as functions of the time t, display distinct decay rates based on whether the height function grows significantly larger (upper tail) or smaller (lower tail) than the expected value. Upper tails exhibit an exponential decay with rate function which we determine explicitly. Conversely, the lower tails experience a more rapid decay and the rate function is given in terms of a variational problem.

Our analysis relies on two inputs. The first is a connection between the height function hand an important measure on the set of integer partitions, the Poissonized Plancherel measure, which stems from nontrivial applications of the celebrated Robinson-Schensted-Knuth correspondence. The second ingredient is the derivation of a priori convexity bounds for the rate function, which combines combinatorial and probabilistic arguments.

This is a joint work with S.Das (Chicago) and Y.Liao (Wisconsin-Madison).

Tuesday, July 2, 2024

Kilian Raschel (Université d’Angers)

Title: A functional equation approach to reflected Brownian motion

Abstract:

The last two decades have seen a flurry of activity around the combinatorial model of walks in the quarter plane. One reason for this is that this model not only occupies a central position in enumerative combinatorics (via bijections with other combinatorial models), but it has also motivated different communities (probability, complex analysis, functional equations, Galois theory, etc.) to work together to develop new techniques and derive new results. While it can be said that walks in the quarter plane are now fairly well understood, a natural question for a probabilist is to study the continuous analogue, namely Brownian motion in a quadrant. It turns out that this model was introduced forty years ago using intrinsically probabilistic methods. In this talk I will explain how delicate probabilistic problems associated with Brownian motion in cones can be solved using functional equations, in particular Galois results on the nature of the solutions to such equations. This talk is based on work with several co-authors, mainly arXiv:2101.01562 and arXiv:2401.10734.

Recording: https://ed-ac-uk.zoom.us/rec/share/qPQYSkFUNkveLKC8fcI3BF9aQpzD0g_oTOpWEPqxaCS0Q_jstqwKOBgr0Bd-_TRX.JiEn7Caou8XvClq3?startTime=1719929213000

Tuesday, May 21, 2024

Evan Sorensen (Columbia University)

Title: Jointly invariant measures for the KPZ equation with periodic noise

Abstract:

We present an explicit coupling of Brownian bridges plus affine shifts that are jointly invariant for the Kardar-Parisi-Zhang equation with periodic noise. These are described as Pitman-like transforms of independent Brownian bridges. We obtain these invariant measures by working with a semi-discrete model known as the O’Connell-Yor polymer in a periodic environment. In that setting, the relevant Markov process is described by a system of coupled SDEs. We show how to transform this Markov process to an auxiliary Markov process with a more tractable invariant measure. We discuss connections of this method to works of Ferrari and Martin in the mid 2000s in the context of multi-species particle systems. Furthermore, we present an application of this work to give an explicit formula for the covariance function of a limiting Gaussian process obtained from the coupled stochastic heat equation. Based on forthcoming joint work with Ivan Corwin and Yu Gu.

Tuesday, May 14, 2024

Lucio Galeati (EPFL)

Title: Propagation of chaos for singular interacting particle systems driven by fBm

Abstract:

Systems of N particles, whose evolution is described by a mean-field pairwise interaction, and are driven by independent Brownian motions, are often expected to converge in the large N limit to solutions of a McKean-Vlasov equation, a non local SDE in the probability space. It is less known, but also classical, that the result is not specific to the drivers being Brownian; as long as the interaction kernel is smooth, the same holds true for a much larger class of processes, like fractional Brownian motion (fBm) of Hurst parameter $H\in (0,1)$ .

This raises the question of understanding what happens for more singular interactions. On one hand, fBm is not Markovian nor a martingale, so Ito calculus and PDE techniques are not available anymore; on the other, it has a strong regularizing effect on standard SDEs, making their analysis possible even for distributional drifts. In this talk, I will present a propagation of chaos result, which holds for a general class of rough interaction kernels whose regularity depends on the value $H$ . The proofs rely on recently developed stochastic sewing techniques.

Based on a joint work with K. Le and A. Mayorcas.

Recording: https://ed-ac-uk.zoom.us/rec/share/8rEsukyeNARWpJaDtaF_X0tEIeRpIdo60Iuhcwxsr9g5L3_dKElvAi98yY5YPNXB.L2oap1KNOrfaiF87?startTime=1715695297000

Michaela Szölgyenyi (University of Klagenfurt)

Title: Bicausal optimal transport for SDEs with irregular coefficients

Abstract:

We solve an optimal transport problem under probabilistic constraints, where the marginals are laws of solutions of stochastic differential equations with irregular, that is non-globally Lipschitz continuous coefficients. Numerical methods are employed as a theoretical tool to bound the adapted Wasserstein distance. This opens the door for computing the adapted Wasserstein distance in a simple way.

Joint work with Benjamin A. Robinson (University of Klagenfurt).

Recording: https://ed-ac-uk.zoom.us/rec/share/8rEsukyeNARWpJaDtaF_X0tEIeRpIdo60Iuhcwxsr9g5L3_dKElvAi98yY5YPNXB.L2oap1KNOrfaiF87?startTime=1715695297000

Tuesday, April 2, 2024

Samuel Johnston(King’s College London)

Title: Free probability via entropic optimal transport

Abstract:

The basic operations of free probability – additive free convolution, multiplicative free convolution, and free compression – describe how the eigenvalues of large random matrices interact under the basic matrix operations, such as addition, multiplication, and taking minors.

In this talk we discuss how these free probability operations can be formulated in terms of an “entropic optimal transport” problem – an optimal transport problem but with an entropy penalty for the coupling measure.

Our proof of this formulation uses the quadrature formulas of Marcus, Spielman and Srivastava, which relate the expected characteristic polynomial of matrices under random unitary vs symmetric conjugation. The approach involves an asymptotic analysis of the quadrature formulas using a large deviation principle on the symmetric group.

This is joint work with Octavio Arizmendi (CIMAT).

Recording: https://ed-ac-uk.zoom.us/rec/share/y_L5vbZgzlhngSxNo4JfxhV0rdDMWLXYwN0yNSaU-kRTyoyBGd00v_a6qns1bSVd.f0nmZS_GfVst3O9o

Tuesday, March 26, 2024

Matthew Rosenzweig (Carnegie Mellon University) [Online]

Title: Fluctuations around the mean-field limit for singular Riesz flows

Abstract:

I will discuss recent work establishing a dynamical central limit theorem for global fluctuations around the mean-field limit of first-order systems with singular log/Riesz interactions with or without noise. Our method is based on studying the evolution of linear statistics along the adjoint flow, which allows us to leverage the machinery of modulated energy and commutator estimates. Time permitting, I will also discuss estimates for the dynamical cumulants of linear statistics and bounds for the time-dependent Ursell (connected correlation) functions, which allow to approximate marginals to arbitrary accuracy in $N$ . Based on joint work with Jiaoyang Huang and Sylvia Serfaty.

Recording: https://ed-ac-uk.zoom.us/rec/share/_P3qSY2tjEzYMbODkkpbS26EYWkUsCrZl8hZ-VAcqpbuRJX2v350KMHvr8w7WPhH.5Jg2hnWr8NnSl5I9?startTime=1711465526000

Tuesday, March 19, 2024

Paweł Duch (Adam Mickiewicz University in Poznań)

Title: Construction of critical fermionic QFTs using Polchinski flow equation

Abstract:

I will present a new technique of constructing fermionic quantum field theories based on the renormalization group flow equation. The technique is applicable to models that are scaling critical and asymptotically free, such as the two-dimensional Gross-Neveu model. The correlation functions of a model are expressed in terms of the effective potential and the effective potential is constructed by solving the flow equation using the Banach fixed point theorem. In order to define a suitable space of functionals, in which the flow equation can be solved, I use the filtered non-commutative probability space introduced in the recent work by De Vecchi, Fresta and Gubinelli. The construction uses crucially the fact that fermionic fields anti-commute and does not generalize to models including bosons.

Recording: https://ed-ac-uk.zoom.us/rec/share/1hvK65Ox_y0VB4CNX6GDuc4qu3g65Po7s__w2tAow8yV-N0G8Too9yhLJdP_V3TN.SNZ2VoN7zl7HQ45y?startTime=1710860458000

Wednesday, March 13, 2024: Maxwell Institute Probability and Stochastic Analysis Workshop

14:00 – 15:00: Massimiliano Gubinelli (University of Oxford) “Stochastic quantisation of the fractional $\Phi^4$ model via flow equations”

15:00 – 16:00: Jordan Stoyanov (Bulgarian Academy of Sciences) “Characterizations of probability distributions: a bunch of old and new results”

16:00 – 16:30: coffee break

16:30 – 17:15: Ofer Busani (University of Edinburgh) “On the number of infinite geodesics in exceptional directions in the KPZ class”

17:15 – 18:00: Paul Dobson (Heriot-Watt University) “Piecewise deterministic sampling with splitting schemes”

Massimiliano Gubinelli (University of Oxford)

Title: Stochastic quantisation of the fractional 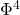$\Phi^4$ model via flow equations

Abstract:

I will describe a recent result obtained in collaboration with P. Rinaldi and P. Duch. We construct the Euclidean fractional \Phi^4 quantum field via the method of stochastic quantisation. This involves obtaining global space-time solutions for a singular stochastic PDE of fractional parabolic type with cubic non-linearity. This goal is achieved via a novel method of flow equations introduced by Duch.

Jordan Stoyanov (Bulgarian Academy of Sciences)

Title: Characterizations of probability distributions: a bunch of old and new results

Abstract:

It is common for any specific distribution, say F, to try to find a property which is valid only for F. In any such a case we talk about a characterizing property and a characterization problem. Well-known are classical results for popular distributions such as Normal, Poisson, Exponential, Geometric, Gamma, etc. (Cramer, Raikov, Polya, Bernstein, Skitovich-Darmois). The work on such problems is going on and some new very recent results will be reported. We can also ask whether or not a distribution can be characterized by its moments, which is one of the fundamental questions in the classical moment problem (Chebyshev, Markov, Stieltjes). Besides well-known results (Hamburger, Hausdorff, Carleman, Hardy, Krein, Lin, rate of growth of moments), some very recent results on M-(in)determinacy of distributions will be presented. Useful illustrations and (sometime) surprising facts for specific continuous and/or discrete distributions will be given. Challenging open questions will be outlined.

Ofer Busani (University of Edinburgh)

Title: On the number of infinite geodesics in exceptional directions in the KPZ class

Abstract:

The KPZ class consists of many models of random growth interface. In many cases, the dynamics of these models can be studied via variational forms that give rise to metric-like spaces, which in turn, can be studied through geodesics. The study of infinite geodesics in the KPZ class has been studied intensively in the past 30 years. One central question is the following:Given a direction, how many infinite geodesics that are asymptotically going in that direction are there?In this talk, I shall discuss what we know about infinite geodesics in the KPZ class and some recent developments regarding the question above.

Based on several works with Marton Balazs, Timo Seppalainen and Evan Sorensen.

Paul Dobson (Heriot-Watt University)

Title: Piecewise deterministic sampling with splitting schemes

Abstract:

Piecewise deterministic Markov processes (PDMPs) received substantial interest in recent years as an alternative to classical Markov chain Monte Carlo algorithms. While theoretical properties of PDMPs have been studied extensively, their practical implementation remains limited to specific applications in which bounds on the gradient of the negative log-target can be derived. In order to address this problem, we propose to approximate PDMPs using splitting schemes and will discuss the properties of this approximation.

Tuesday, March 5, 2024

Michela Ottobre (Heriot-Watt University)

Title: McKean-Vlasov S(P)Des with additive noise

Abstract:

Many systems in the applied sciences are made of a large number of particles. One is often not interested in the detailed behaviour of each particle but rather in the collective behaviour of the group. An established methodology in statistical mechanics and kinetic theory allows one to study the limit as the number of particles N tends to infinity and to obtain a (low dimensional) PDE for the evolution of the density of particles. The limiting PDE is a non-linear equation, where the non-linearity has a specific structure and is called a McKean-Vlasov nonlinearity. Even if the particles evolve according to a stochastic differential equation, the limiting equation is deterministic, as long as the particles are subject to independent sources of noise. If the particles are subject to the same noise (common noise) then the limit is given by a Stochastic Partial Differential Equation (SPDE). In the latter case the limiting SPDE is substantially the McKean-Vlasov PDE + noise; noise is further more multiplicative and has gradient structure. One may then ask the question about whether it is possible to obtain McKean-Vlasov SPDEs with additive noise from particle systems. We will explain how to address this question, by studying limits of weighted particle systems, in a framework introduced by Kurtz and collaborators.

This is a joint work with L. Angeli, D. Crisan, M. Kolodziejzik.

Recording: https://ed-ac-uk.zoom.us/rec/share/lwjEWTKFabOMIbfB4_ItWH60_503ucW4LSp2Kbuew400UpUx57iT42QPs8ByyeGw.0FChtECophMD0TVx?startTime=1709650952000

William Salkeld(University of Nottingham)

Title: Locally interacting equations and their associated McKean-Vlasov marginal

Abstract:

In this talk, I will discuss the dynamics of a collection of Gaussian stochastic differential equations indexed by a locally finite graph. The drift of each individual equation is dependent only on the dynamics of the individual and their neighbours so that each SDE exhibits strong correlation with a small number of other SDEs via these local interactions.

Such local interactions arise in statistical physics, engineering and simulation of SPDEs, and are suitable for applications when long range interactions between distant individuals are described via a sequence of local interactions between neighbours. We will focus on simulation of the Allen-Cahn equation.

The price we pay for considering local interactions instead of macroscopic ‘mean-field’ interactions is that the when the number of equations is large we do not expect the statistical decoupling of any pair of equations. Instead, the dynamics exhibit a ‘Markov Random Field’ property where equations are conditionally independent of one another conditioning on an appropriate separating subset.

Further, these systems of equations are continuously dependent on the underlying graph structure so that changes in the interactions leads to proportional changes in the all equations.

These fundamental properties of the entire system of equations is key to understanding the microscopic dynamics of each individual equation, and deriving a McKean-Vlasov equation that describes the marginal distribution of local neighbourhoods.

This is based on joint work with Kavita Ramanan and Kevin Hu.

Recording: https://ed-ac-uk.zoom.us/rec/share/lwjEWTKFabOMIbfB4_ItWH60_503ucW4LSp2Kbuew400UpUx57iT42QPs8ByyeGw.0FChtECophMD0TVx?startTime=1709654612000

Tuesday, February 27, 2024

Larisa Yaroslavtseva (University of Graz)

Title: On the complexity of strong approximation of SDEs with a non-Lipschitz drift coefficient

Abstract:

We study pathwise approximation of stochastic differential equations (SDEs) at a single time based on finitely many (sequential) evaluations of the driving Brownian motion. The classical assumption in the literature on numerical approximation of SDEs is global Lipschitz continuity of the coefficients of the equation. However, many SDEs arising in applications fail to have globally Lipschitz continuous coefficients. In this talk we focus on the case when the drift coefficient is not Lipschitz continuous. In particular, we discuss recent results on corresponding upper and lower error bounds for SDEs with a drift coefficient that satisfies piecewise smoothness assumptions or has fractional Sobolev regularity.

The talk is based on joint work with Simon Ellinger (University of Passau), Arnulf Jentzen (Univerity of M¨unster) and Thomas M¨uller-Gronbach (University of Passau).

Recording: https://ed-ac-uk.zoom.us/rec/share/uKMLSVleFjRKvAx2R7DXsXtP8hfkyqBCz_MJ8lyBj6eovAuCUCVjkoLGWNBkKAx0.j3ggf6Oo1i9p4Ayx?startTime=1709046302000

Tuesday, February 20, 2024

Zhenfu Wang (BICMR-Peking University) [Online]

Title: Quantitative Propagation of Chaos for 2D Viscous Vortex Model on the Whole Space

Abstract:

We derive the quantitative estimates of propagation of chaos for the large interacting particle systems in terms of the relative entropy between the joint law of the particles and the tensorized law of the mean field PDE. We resolve this problem for the first time for the viscous vortex model that approximating 2D Navier-Stokes equation in the vorticity formulation on the whole space. We obtain as key tools the Li-Yau-type estimates and Hamilton-type heat kernel estimates for 2D Navier-Stokes on the whole space. This is based on a joint work with Xuanrui Feng from Peking University.

Recording: https://ed-ac-uk.zoom.us/rec/share/PIa7SwzkDrg1B0dD8nZGfq8p0YE_EG2WNzaoqaH8qGqNza7hFhzge3OWZDyt4P3t.CUJFgl03kh_4FCi5?startTime=1708438042000

Renyuan Xu (University of Southern California) [Online]

Title: Some Mathematical Results on Generative Diffusion Models

Abstract:

Generative diffusion models, which transform noise into new data instances by reversing a Markov diffusion process in time, have become a cornerstone in modern generative models. A key component of these models is to learn the associated Stein’s score function. While the practical power of diffusion models has now been widely recognized, the theoretical developments remain far from mature. Notably, it remains unclear whether gradient-based algorithms can learn the score function with a provable accuracy. In this talk, we develop a suite of non-asymptotic theory towards understanding the data generation process of diffusion models and the accuracy of score estimation. Our analysis covers both the optimization and the generalization aspects of the learning procedure, which also builds a novel connection to supervised learning and neural tangent kernels.

This is based on joint work with Yinbin Han and Meisam Razaviyayn (USC).

Recording: https://ed-ac-uk.zoom.us/rec/share/YNMOd88SVPWpvpFvNCljCFp-YfMccq4laAtg7IzgylUbsxllK5z-PdPcyc9nxtDs.kpwQrdgae549VOYA?startTime=1708441675000

Tuesday, February 13, 2024

Oana Lang (Imperial College London)

Title: Local and global existence for transport and non-transport SPDEs

Abstract:

This talk will be focused on local and global properties for a class of stochastic partial differential equations (SPDEs) which includes equations coming from geophysical fluid dynamics. There are many SPDEs in the literature for which global existence of solutions does not hold, with several such examples coming from fluid dynamics. This has important consequences not just analytically, but also in applications. I will discuss conditions under which such equations can admit existence of a global solution and implications at their structural level. This is joint work with Dan Crisan.

Recording: https://ed-ac-uk.zoom.us/rec/share/J1Lc8YyCONpp9Cy602FpqqT5n1WyEISu3fY_fVjHDGXZM2A0GAd9BLDgYXT95j6z.YxyBCoJ2f0Il–PA?startTime=1707836717000

Tuesday, February 6, 2024

Johannes Muhle-Karbe (Imperial College London)

Title: Optimal Contracts for Delegated Order Execution

Abstract:

We determine the optimal contract for a client who delegates their order execution to a dealer. Existence and uniqueness are established for general linear price impact dynamics of the dealer’s trades. Explicit solutions are available for the model of Obizhaeva and Wang, for example, and a simple gradient descent algorithm is applicable in general. The optimal contract allows the client to almost achieve the first-best performance without any agency conflicts. Common trading arrangements arise as limiting cases. In particular, optimal contracts for many reasonable model parameters resemble the “fixing contract” common in FX markets, in that they only incorporate market prices briefly before the conclusion of the trade. Price manipulation by the dealer is avoided by only putting a sufficiently small weight on these prices, and complementing this part of the contract with a sufficiently large fixed fee. (Joint work with Martin Larsson and Benjamin Weber).

PREPRINT: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4621546

Recording: https://ed-ac-uk.zoom.us/rec/share/G5xEakyCo9vnyOJKtjIIoj81hLzTQQaJuj-7VacLZtysU2mxvslzATs0qMYivHoh.WpYwbShVtrbRLdBp

Tuesday, January 30, 2024

Ying Zhang (The Hong Kong University of Science and Technology (Guangzhou))

Title: Langevin dynamics-based algorithm e-THeO POULA for stochastic optimization with discontinuous stochastic gradient

Abstract:

We introduce a new Langevin dynamics-based algorithm, called e-THO POULA, to solve optimization problems with discontinuous stochastic gradients which naturally appear in real-world applications such as quantile estimation, vector quantization, CVaR minimization, and regularized optimization problems involving ReLU neural networks. We demonstrate both theoretically and numerically the applicability of the e-THO POULA algorithm. More precisely, under the conditions that the stochastic gradient is locally Lipschitz in average and satisfies a certain convexity at infinity condition, we establish non-asymptotic error bounds for e-THeO POULA in Wasserstein distances and provide a non-asymptotic estimate for the expected excess risk, which can be controlled to be arbitrarily small. Two key applications in finance are provided, namely, multi-period portfolio optimization and transfer learning in multi-period portfolio optimization, which involve neural networks with (Leaky)-ReLU activation functions. Numerical experiments conducted using real-world datasets illustrate the superior empirical performance of e-THeO POULA compared to SGLD, ADAM, and AMSGrad in terms of model accuracy.

Recording: https://ed-ac-uk.zoom.us/rec/share/w06TSKfqlf2thqEKqBhWuXjvLFhQ-hmNwaRFk9hNbKFHCs74zDXzjtBM4gVTeJcD.SdlrZvqte4vYB0Vn

Tuesday, January 23, 2024

Xell Brunet Guasch (University of Edinburgh)

Title: Multi-Type Critical Birth-Death Process: A Model of Error-Induced Extinction

Abstract:

Extreme mutation rates in microbes and cancer cells can result in error-induced extinction (EEX), where every descendant cell eventually acquires a lethal mutation. In this work, we investigate critical birth-death processes with n distinct types as a birth-death model of EEX in a growing population. Each type i cell divides independently or mutates at the same rate. The total number of cells grows exponentially as a Yule process until a cell of type n appears, which cell type can only die at rate one. This makes the whole process critical and hence after the exponentially growing phase eventually all cells die with probability one.

We present large-time asymptotic results for the general n-type critical birth-death process. We find that the mass function of the number of cells of type k has algebraic and stationary tail, in sharp contrast to the exponential tail of the first type. The same exponents describe the tail of the asymptotic survival probability . We discuss applications of the results for studying extinction due to intolerable mutation rates in biological populations.

Tuesday, January 16, 2024

Catherine Wolfram (MIT) [Online]

Title: The dimer model in 3D

Abstract:

A dimer tiling of Z^d is a collection of edges such that every vertex is covered exactly once. In 2000, Cohn, Kenyon, and Propp showed that 2D dimer tilings satisfy a large deviations principle. In joint work with Nishant Chandgotia and Scott Sheffield, we prove an analogous large deviations principle for dimers in 3D. A lot of the results for dimers in two dimensions use tools and exact formulas (e.g. the height function representation of a tiling or the Kasteleyn determinant formula) that are specific to dimension 2. I will explain how to formulate the large deviations principle in 3D, show simulations, try to give some intuition for why three dimensions is different from two. Time permitting, I will explain some of the ways that we use a smaller set of tools (e.g. Hall’s matching theorem or a double dimer swapping operation) in our arguments.

Recording: https://ed-ac-uk.zoom.us/rec/share/-jcTP95esz28ClvM6LR7em0Q89VBjZTc38zvdPPb_Cf0dRddVwzZl1WwgRFF6urz.WMrTUWhKTGCdWiqy?startTime=1705417460000

Tuesday, December 5, 2023

Maxim Raginsky (University of Illinois at Urbana-Champaign) [Online]

Title: A variational approach to sampling and path estimation in diffusion processes

Abstract:

Recently, diffusion models have achieved remarkable breakthroughs in generative modeling, with practical advances outpacing theoretical understanding. This has led to a surge of interest in the theory of diffusion processes, as well as in the fundamental links between stochastic control, nonequilibrium thermodynamics, and learning. In this talk, I will present a unified perspective on sampling, inference, and path estimation (or smoothing) in diffusion processes through the lens of free energy minimization. This variational perspective ties together the Gibbs variational principle with the Cameron-Martin-Girsanov change of measure and the Hamilton-Jacobi-Bellman optimal control formulation. Several existing results emerge as special cases, including the variational formulation of nonlinear estimation due to Newton and Mitter and the recent control-theoretic derivation of diffusion-based generative modeling due to Berner, Richter, and Ullrich.

Recording: https://ed-ac-uk.zoom.us/rec/share/V_WoveUSQw2hbFLCpXB3a3Nrp6gDvITGBdlt8pOQPb4l6xfHjNfjbx_yRdq_ZhP5.Oi0nkHAUIK7F67WX?startTime=1701795918000

Corrected Slides: Raginsky.pdf

Tuesday, November 28, 2023

Sarah-Jean Meyer(University of Oxford)

Title: The forward-backward approach to the sine-Gordon EQFT

Abstract:

We present a forward-backward approach to stochastic quantisation for the sine-Gordon Euclidean quantum field $\cos(\beta\phi)_2$ on the full space up to the second threshold, i.e. for $\beta^2<6\pi$ . The basis of our method is a forward-backward stochastic differential equation (FBSDE) for a decomposition $(X_t)_{(t\geq 0)}$ of the interacting Euclidean field $X_\infty$ along a scale parameter $t\geq 0$ . This FBSDE describes the optimiser of a stochastic control representation of the Euclidean QFT introduced by Barashkov and Gubinelli and provides a scale-by-scale description of the interacting field without cut-offs. I will present the general idea of the approach, and illustrate how the FBSDE can be used effectively to study the sine-Gordon measure to obtain results such as large deviations, integrability, decay of correlations for local observables, Osterwalder–Schrader axioms and other properties.

This talk is based on joint work with Massimiliano Gubinelli.

Recording: https://ed-ac-uk.zoom.us/rec/share/t4ikDGAGyt2vqetWobo94R7LhetZw7Wi578MU-Y_C9Yfa0D-Q-aQN_UA3P6ogwtP.Jwiu1AsAtEadOrUS?startTime=1701184125000

Tuesday, November 21, 2023

Gal Kronenberg (University of Oxford)

Title: Independent sets in random subgraphs of the hypercube

Abstract:

Independent sets in bipartite regular graphs have been studied extensively in combinatorics, probability, computer science and more. The problem of counting independent sets is particularly interesting in the d-dimensional hypercube $\{0,1\}^d$ , motivated by the lattice gas hardcore model from statistical physics. Independent sets also turn out to be very interesting in the context of random graphs.

The number of independent sets in the hypercube $\{0,1\}^d$ was estimated precisely by Korshunov and Sapozhenko in the 1980s and recently refined by Jenssen and Perkins.

In this talk we will discuss new results on the number of independent sets in a random subgraph of the hypercube. The results extend to the hardcore model and rely on an analysis of the antiferromagnetic Ising model on the hypercube.

This talk is based on joint work with Yinon Spinka.

Recording: https://ed-ac-uk.zoom.us/rec/share/J9ntMHtJppAtM55sLyzXTTo1DjFZVD8iYBSvZ6kGno3YaM5cTwMRSsoCjkE0pEdf.uX_Jko8q4mGJQTpz?startTime=1700579113000

Tuesday, November 14, 2023

Nikolas Nüsken (King’s College London)

Title: Transport meets Variational Inference: Controlled Monte Carlo Diffusions

Abstract:

Connecting optimal transport and variational inference, this talk is about a principled and systematic framework for score-based sampling and generative modelling centred around forward and reverse-time stochastic differential equations. In particular, I will discuss the novel Controlled Monte Carlo Diffusion (CMCD) methodology for Bayesian computation, a score-based annealing technique that crucially adapts both forward and backward dynamics in a diffusion model. Time permitting, we will discuss relationships to optimal control and Schroedinger bridges, as well as connections to the Jarzinsky and Crooks identities from statistical physics. This is joint work with F. Vargas, S. Padhy and D. Blessing.

Recording: https://ed-ac-uk.zoom.us/rec/share/YKYXMSOiQ_EW_wOJvHEq7PbpCnnjGeADrjMCyveBlQR6tVQFIKjUWn2W14HV88QO.SYTMM1VEXqivgINd?startTime=1699974089000

Tuesday, November 7, 2023

Harprit Singh (University of Edinburgh)

Title: Singular SPDEs on Geometric Spaces

Abstract:

We shall discuss the solution theory to a large class of singular SPDEs in various nontranslation invariant settings. In particular, I shall present results on Riemannian manifolds and homogeneous Lie groups as well as related results for non-translation invariant parabolic and hypo-elliptic equations on Euclidean space. Based on joint work with M. Hairer, respectively A. Mayorcas.

Recording: https://ed-ac-uk.zoom.us/rec/share/nKLKyNdwEAtl0Go0zYAz_Q5OMMUWOcGdbMN62LjNZTM8k0DWeFJpp65Z78QDt7Rf.DTFAM_EnbUwY2SKQ?startTime=1699369338000

Tuesday, October 31, 2023

Guillaume Barraquand (ENS)

Title: Stationary measures in the Kardar-Parisi-Zhang universality class

Abstract:

The Kardar-Parisi-Zhang (KPZ) equation is a nonlinear stochastic PDE introduced in Physics to model interface growth. In one dimension, the KPZ equation on the line admits a remarkably simple stationary measure: the Brownian motion. For the KPZ equation on an interval or a half-line, however, stationary measures are non-Gaussian and depend on the boundary conditions imposed. Their explicit description has been obtained only very recently, through the detailed study of integrable probabilistic models, such as ASEP or directed polymer models, that can be viewed as discretizations of the KPZ equation. We will first review these results, which are based on a series of works by several groups of authors. I will then outline a new method to compute the stationary distributions of stochastic integrable models on a lattice such as last passage percolation, or directed polymer models.

Recording: https://ed-ac-uk.zoom.us/rec/share/xdlF4Wpn0gDV7emqoxBpO77hs5xHUT-c_r0RmfIXFD1EsTx8K_oQ8G0NwrMWC-Qc.I5LYrdx6Bt3z3uwm?startTime=1698764336000

Tuesday, October 24, 2023

Roger Van Peski (KTH)

Title: New local limits in discrete random matrix theory

Abstract:

Random matrices over finite fields, integers, and p-adic integers have been studied since the late 1980s as natural models for random groups appearing in number theory and combinatorics. Recently it has also become clear that the theory has close structural parallels with singular values of complex random matrices, bringing new techniques from integrable probability and motivating new questions. In particular, in this talk I will explain recent results on the local limits of products of such matrices, which yield a new object that may be viewed as a discrete and non-determinantal analogue of (certain deformations of) the extended sine and Airy processes in classical random matrix theory.

Tuesday, October 17, 2023

Ioannis Gasteratos (Imperial College London)

Title: Large deviations of slow-fast systems driven by fractional Brownian motion

Abstract:

We consider a multiscale system of stochastic differential equations in which the slow component is perturbed by a small fractional Brownian motion with Hurst index $H > 1/2$ and the fast component is driven by an independent Brownian motion. Working in the framework of Young integration, we use tools from fractional calculus and weak convergence arguments to establish a Large Deviation Principle (LDP) in the homogenized limit, as the noise intensity and time-scale separation parameters vanish at an appropriate rate. Our approach is based in the study of the limiting behavior of an associated controlled system. We show that, in certain cases, the non-local rate function admits an explicit non-variational form. The latter allows us to draw comparisons to the case $H = 1/2$ which corresponds to the classical Freidlin-Wentzell theory. Moreover, we study the asymptotics of the rate function as $H \to 1/2^+$ and show that it is discontinuous at $H = 1/2$ .

Recording: https://ed-ac-uk.zoom.us/rec/share/juOFLFlyjD9euEmx4iHz_J08Fw60svbT-fSjWWdcF-oXv4wftFjDvh2ml-xWzqtE.TNh28a_znXXtWGb7?startTime=1697551167000

Tuesday, October 10, 2023

Raphaël Maillet (CEREMADE) [Online]

Title: Stochastic McKean-Vlasov Equation with common noise

Abstract:

In this talk, we explore the long-term behaviour of solutions to a nonlinear McKean-Vlasov equation with common noise. This equation arises naturally when studying the collective behaviour of interacting particles driven by both individual and common noise. Our main focus is to understand how the presence of common noise affects the stability of the system. We will first present the results for the case without common noise and then discuss how the introduction of common noise can enhance stability in certain respects.

Recording: https://ed-ac-uk.zoom.us/rec/share/YLc3o8xHsc3UBWLzhpvbDw8i48lkHb7zzBJEv7zYVUUIGiCLWW38IaAYbyuJ1mk.x9yT7TxcGMHL_LyU?startTime=1696946479000

Tuesday, October 3, 2023

Kohei Suzuki (Durham University)

Title: Curvature Bound of the Dyson Brownian Motion

Abstract:

The Dyson Brownian Motion (DBM) is an eigenvalue process of a particular Hermitian matrix-valued Brownian motion introduced by Freeman Dyson in 1962, which has been one of the central subjects in the random matrix theory. In this talk, we study the DBM from a geometric perspective. We show that the infinite particle DBM possesses a lower bound of the Ricci curvature à la Bakry-Émery. As a consequence, we obtain various quantitative estimates of the transition probability of the DBM (e.g., the local spectral gap, the local log-Sobolev, and the dimension-free Harnack inequalities) as well as the characterisation of the DBM as the gradient flow of the Boltzmann entropy in a particular Wasserstein-type space.

Recording: https://ed-ac-uk.zoom.us/rec/share/RtRMgSoJBWaRxSOgjK_ZvmGY-CwCEPWOPI38zl4ZxasGMIMpdrZ3jKANDeHfKus9.Fz_cFkVMbNO1wOK_?startTime=1696341809000

September 26, 2023

Ofer Busani (University of Edinburgh)

Title: Scaling limit of multi-type stationary measures in the KPZ class

Abstract:

The KPZ class is a very large set of $1+1$ models that are meant to describe random growth interfaces. It is believed that upon scaling, the long time behavior of members in this class is universal and is described by a limiting random object, a Markov process called the KPZ fixed-point. The (one-type) stationary measures for the KPZ fixed-point as well as many models in the KPZ class are known – it is a family of distributions parametrized by some set $I_{ind}$ that depends on the model. For $k\in \mathbb{N}$ the k-type stationary distribution with intensities $\rho_1,...,\rho_k \in I_{ind}$ is a coupling of one-type stationary measures of indices $\rho_1,...,\rho_k$ that is stationary with respect to the model dynamics. In this talk we will present recent progress in our understanding of the multi-type stationary measures of the KPZ fixed-point as well as the scaling limit of multi-type stationary measures of two families of models in the KPZ class: metric-like models (e.g. last passage percolation) and particle systems (e.g. exclusion process). Based on joint work with Timo Seppalainen and Evan Sorensen.

June 14, 2023

Yufei Zhang (LSE)

Title: Exploration-exploitation trade-off for continuous-time reinforcement learning

Abstract:

Recently, reinforcement learning (RL) has attracted substantial research interests. Much of the attention and success, however, has been for the discrete-time setting. Continuous-time RL, despite its natural analytical connection to stochastic controls, has been largely unexplored and with limited progress. In particular, characterising sample efficiency for continuous-time RL algorithms remains a challenging and open problem.

In this talk, we develop a framework to analyse model-based reinforcement learning in the episodic setting. We then apply it to optimise exploration-exploitation trade-off for linear-convex RL problems, and report sublinear (or even logarithmic) regret bounds for a class of learning algorithms inspired by filtering theory. The approach is probabilistic, involving analysing learning efficiency using concentration inequalities for correlated continuous-time observations, and applying stochastic control theory to quantify the performance gap between applying greedy policies derived from estimated and true models.

May 3, 2023: North British Probability Workshop

Neil O’Connell (University College Dublin) [Online]

Title: A Markov chain on reverse plane partitions

Abstract:

I will discuss a natural Markov chain on reverse plane partitions

which is closely related to the Toda lattice.

Recording: https://ed-ac-uk.zoom.us/rec/share/PtOJha0k1NPgeNe5kdjiVCNxQOlNqC5d_3oCH2lAjBTERBvljw_CdgtSmVwnm46e.muM4n4W9-6olY6GA

Athanasios Vasileiadis (University of Nice)

Title: Learning linear quadratic Mean Field Games.

Abstract:

In this talk we are going to use common noise as a form of exploration to learn the Nash equilibrium of a Linear Quadratic Mean Field Game. We develop a scheme based on Fictitious Play and study its convergence to the analytical solution of the limit system. We illustrate the analysis by numerical implementations using regression on a basis of Hermit polynomials and also artificial neural networks.

Recording: https://ed-ac-uk.zoom.us/rec/share/U6UmjO9M6cvpULjTi1balg3UvtFQy-C0pueruoivPCYvWUmeboa1k_0rVi9a5HM.f7EkReDHRV5W0lPH

Stefano Bruno (University of Edinburgh)

Title: Optimal Regularity in Time and Space for Stochastic Porous Medium Equations

Abstract:

Stochastic porous medium equations are well-studied models describing non-linear diffusion dynamics perturbed by noise. In this talk, we consider the noise to be multiplicative, white in time and coloured in space and the diffusion coefficients to be Hölder continuous. Our assumptions include the cases of smooth coefficients of, at most, linear growth as well as $\sqrt{u}$ – coefficients relevant in population dynamics. Using the kinetic solution theory for conservation laws, we prove optimal regularity estimates consistent with the optimal regularity derived for the deterministic porous medium equation in Gess (JEMS, 2020) and Gess, Sauer, Tadmor (APDE, 2020) and the presence of the temporal white noise. The proof of our result relies on a significant adaptation of velocity averaging techniques from their usual $L^1$ context to the natural $L^2$ setting of the stochastic case. This is joint work with Benjamin Gess and Hendrik Weber.

Recording: https://ed-ac-uk.zoom.us/rec/share/U6UmjO9M6cvpULjTi1balg3UvtFQy-C0pueruoivPCYvWUmeboa1k_0rVi9a5HM.f7EkReDHRV5W0lPH

April 26, 2023:

Benjamin Fehrman (University of Oxford)

Title: Non-equilibrium fluctuations and parabolic-hyperbolic PDE with irregular drift

Abstract:

Non-equilibrium behavior in physical systems is widespread. A statistical description of these events is provided by macroscopic fluctuation theory, a framework for non-equilibrium statistical mechanics that postulates a formula for the probability of a space-time fluctuation based on the constitutive equations of the system. This formula is formally obtained via a zero noise large deviations principle for the associated fluctuating hydrodynamics, which postulates a conservative, singular stochastic PDE to describe the system far-from-equilibrium. In this talk, we will focus particularly on the fluctuations of the zero range process about its hydrodynamic limit. We will show how the associated MFT and fluctuating hydrodynamics lead to a class of conservative SPDEs with irregular coefficients, and how the study of large deviations principles for the particles processes and SPDEs leads to the analysis of parabolic-hyperbolic PDEs in energy critical spaces. The analysis makes rigorous the connection between MFT and fluctuating hydrodynamics in this setting, and provides a positive answer to a long-standing open problem for the large deviations of the zero range process.

Recording: https://ed-ac-uk.zoom.us/rec/share/3i0gdxTDkkqI4oDR-OR9JKAj_0LaAL4Vuoeki6SPOOWhGe2TRUmwcgvPtg-24TkH.5ar1OvGDnqrGXEUo

April 19, 2023:

Patrik Ferrari (University of Bonn)

Title: Space-time correlations in the KPZ universality class

Abstract:

We consider models in the Kardar-Parisi-Zhang universality class of stochastic growth models in one spatial dimension. We study the correlations in space and time of the height function. In particular we present results on the decay of correlations of the spatial limit processes and on the universality of the first order of the covariance at macroscopically close times.

Recording: https://ed-ac-uk.zoom.us/rec/share/TE70TZkOomtJPuzZzQbM1cv3B5dl1cZowwDWjvPPlezJI0ryvySyFANfHi8tF8mN.4dBa1PTDRP02Pl1t?startTime=1681912646000

March 29, 2023:

Mao Fabrice Djete (École Polytechnique) [Online]

Title: Non–regular McKean–Vlasov equations and calibration problem in local stochastic volatility models

Abstract:

In this talk, motivated by the calibration problem in local stochastic volatility models, we will investigate some McKean–Vlasov equations beyond the usual requirement of continuity of the coefficients in the measure variable for the Wasserstein topology. We will provide first an existence result for this type of McKean–Vlasov equations and explain the main idea behind the proof. In a second time, we will show an approximation by particle system for this type of equations, a result almost never rigorously proven in the literature in this context.

Recording: https://ed-ac-uk.zoom.us/rec/share/UCav231Kx_fHc0Lc_v_dw_CxNRMbeHNFXuRATW2F6pxsVYT-v_2HSIoXY-1PTjaa.OmjpNkASe9pORBBT?startTime=1680098573000

Christian Bayer (WIAS Berlin) [Online]

Title: Optimal stopping with signatures

Abstract:

We propose a new method for solving optimal stopping problems (such as American option pricing in finance) under minimal assumptions on the underlying stochastic process X.
We consider classic and randomized stopping times represented by linear and non-linear functionals of the rough path signature $\mathbb{X}<\infty$ associated to X, and prove that maximizing over these classes of signature stopping times, in fact, solves the original optimal stopping problem. Using the algebraic properties of the signature, we can then recast the problem as a(deterministic) optimization problem depending only on the (truncated) expected signature. By applying a deep neural network approach to approximate the non-linear signature functionals, we can efficiently solve the optimal stopping problem numerically.

The only assumption on the process X is that it is a continuous (geometric) random rough path. Hence, the theory encompasses processes such as fractional Brownian motion, which fail to be either semi-martingales or Markov processes, and can be used, in particular, for American-type option pricing in fractional models, e.g. of financial or electricity markets. (Based on joint work with Paul Hager, Sebastian Riedel, and John Schoenmakers)

Recording: https://ed-ac-uk.zoom.us/rec/share/UCav231Kx_fHc0Lc_v_dw_CxNRMbeHNFXuRATW2F6pxsVYT-v_2HSIoXY-1PTjaa.OmjpNkASe9pORBBT?startTime=1680102531000

March 15, 2023:

Guangqu Zheng (University of Liverpool)

Title: Pathwise local well-posedness of stochastic nonlinear Schrödinger equations with multiplicative noises.

Abstract:

In this talk, I will present a recent work on the stochastic nonlinear Schrödinger equation (SNLS) with multiplicative noises. The equation was first proposed in physics literature, and has attracted much attention in the mathematical community. It has been studied by various researchers such as de Bouard, Debussche, Barbu, Röckner, either in Ito framework or via specific transform. As a result, it is not pathwise. The major difficulty towards a pathwise theory lies at how to give a meaning to the product of the noise and an unknown in presence of deficiency of temporal regularities. Despite some development in the parabolic setting by Gubinelli-Tindel (2010) and by Hairer-Pardoux (2015), the dispersive problem remains unsolved.

In this talk, I will present a joint work with T. Oh (Edinburgh), which established the first pathwise local well-posedness result for SNLS with multiplicative noises in the spatially smooth setting. This work exploits Gubinelli-Tindel’s framework of algebraic integration, in combination with random matrix/tensor estimates from a recent work by Deng-Nahmod-Yue (2022), and in particular, the notion of operator-valued controlled rough paths adapted to the Schrödinger flow is introduced.

March 8, 2023:

Emanuela Gussetti (Universität Bielefeld)

Title: An application of rough paths theory to the study of the stochastic Landau-Lifschitz-Gilbert equation

Abstract:

The Landau-Lifschitz-Gilbert equation is a model describing the magnetisation of a ferromagnetic material. The stochastic model is studied to observe the role of thermal fluctuations. We interpret the linear multiplicative noise appearing by means of rough paths theory and we study existence and uniqueness of the solution to the equation on a one dimensional domain $D$ . As a consequence of the rough paths formulation, the map that to the noise associates the unique solution to the equation is locally Lipschitz continuous in the strong norm $L^\infty([0,T];H^1(D))\cap L^2([0,T];H^2(D))$ . This implies a Wong-Zakai convergence result, a large deviation principle, a support theorem.

We prove also continuity with respect to the initial datum initial datum in $H^1(D)$ , which allows to conclude the Feller property for the associated semigroup. We also discuss briefly a Path-wise central limit theorem and a moderate deviations principle for the stochastic LLG: in this case the rough paths formulation leads to a path-wise convergence, not easily reachable in the classical It $\^o$ ‘s calculus setting.

The talk is based on a joint work with A. Hocquet [https://arxiv.org/abs/2103.00926] and on [https://arxiv.org/abs/2208.02136].

Recording: https://ed-ac-uk.zoom.us/rec/share/NqgUULB9KL3wRdB8YFe6VZosZn-62-YCMOggGmLgqEdmrtntXRddzTdjPmpITqE0.6AiqbM7rditaTm6k

February 15, 2023:

Laure Dumaz (ENS)

Title: Some aspects of the Anderson Hamiltonian in 1D.

Abstract:

In this talk, I will present several results on the Anderson Hamiltonian with white noise potential in dimension 1. This operator formally writes « – Laplacian + white noise ». It arises as the scaling limit of various discrete models and its explicit potential allows for a detailed description of its spectrum. We will discuss localization of its eigenfunctions as well as the behavior of the local statistics of its eigenvalues. Around large energies, we will see that the eigenfunctions are delocalized and follow a universal shape given by the exponential of a Brownian motion plus a drift, a behavior already observed by Rifkind and Virag in tridiagonal matrix models. Based on joint works with Cyril Labbé.

February 8, 2023:

Fabian Germ (University of Edinburgh)

Title: On conditional densities of partially observed jump diffusions

Abstract: I will present the filtering problem for a partially observed jump diffusion system Z=(X,Y) driven by Wiener processes and Poisson martingale measures. We will derive the filtering equations, describing the time evolution of the normalised conditional distribution and the unnormalised conditional distribution of the unobservable signal X t given the observations Y. Recent results on L_p-calculus for systems with jumps have made it possible to prove existence and regularity properties of (unnormalised) conditional densities in certain Sobolev spaces under fairly general assumptions. We will see such conditions and derive existence and regularity results based on SPDEs for the (unnormalised) conditional density processes.

This is joint work with Istvan Gyongy.

Recording: https://ed-ac-uk.zoom.us/rec/share/5uXeGb84iHFMOpq_GOgZyUgL94dzfYx9Xq5DNsAnrOq4dVVqgexFX0CYTUcoNAIE.lsJ9WNK-nN5QZ7w7

November 24, 2022

Mo Dick Wong (Durham University)

Title: What can we hear about the geometry of an LQG surface?

Abstract: The Liouville quantum gravity (LQG) surface, formally defined as a 2-dimensional Riemannian manifold with conformal factor being the exponentiation of a Gaussian free field, is closely related to random planar geometry as well as scaling limits of models from statistical mechanics. In this talk we consider the bounded, simply connected setting, and explain the Weyl’s law for the asymptotics of the eigenvalues of the (random) Laplace-Beltrami operator. Our approach is purely probabilistic and relies on the study of the so-called Liouville Brownian motion, the canonical diffusion process on an LQG surface. This is a joint work with Nathanael Berestycki.

James Foster (University of Bath) -online talk

Title: High order splitting methods for stochastic differential equations

Abstract: In this talk, we will discuss how ideas from rough path theory can be leveraged to develop high order numerical methods for SDEs. To motivate our approach, we consider what happens when the Brownian motion driving an SDE is replaced by a piecewise linear path. We show that this procedure transforms the SDE into a sequence of ODEs – which can then be discretized using an appropriate ODE solver. Moreover, to achieve a high accuracy, we construct these piecewise linear paths to match certain “iterated” integrals of the Brownian motion. At the same time, the ODE sequences obtained from this path-based approach can be interpreted as a splitting method, which neatly connects our work to the existing literature. For example, we show that the well-known Strang splitting falls under this framework and can be modified to give an improved convergence rate. We will conclude the talk with a couple of examples, demonstrating the flexibility and convergence properties of our methodology.

(joint work with Gonçalo dos Reis and Calum Strange)

Recording: https://ed-ac-uk.zoom.us/rec/share/uButTuqdAo8UX9g7sAdxsqVvyrtZZD229GFD5dcDmkpXchz8LdiTnn4cwTdQmUeF.HYlI6rng5spV3jEN

November 17, 2022

Jiawei Li (University of Edinburgh)

Title: On distributions of random vorticity and velocity fields in turbulent flows

Abstract: In this talk, we are interested in the vorticity and velocity random fields of turbulent flows. I will introduce the evolution equations for probability density functions of these random fields under some conditions on the flow. I will also talk about several methods we used to solve these PDF PDEs numerically. Based on joint works with Zhongmin Qian and Mingrui Zhou.

Recording: https://ed-ac-uk.zoom.us/rec/share/o3IpQRfmxuAFsIftwzB_s1MSKQLH1BgGfZWT5YOsTjxTck9eNwhYfl77Wzj3HaBw.GygPxXqkjSXhQ5NC

November 10, 2022

Mustazee Rahman (Durham University)

Title: Scaling limit of the second class particle

Abstract: The totally asymmetric simple exclusion process (TASEP) is a microscopic analogue of Burgers equation. The characteristics of Burgers equation play an important role in its solution. The second class particle in TASEP mirrors the role of a microscopic characteristic. Although much is known about the macroscopic behaviour of the second class particle, it is of interest to understand its fluctuations. I will discuss the behaviour of the second class particle when the initial conditions of TASEP converge under KPZ scaling. The second class particle has a scaling limit, which can be described in terms of geometric concepts arising in the KPZ universality class. Joint work with Balint Virag.

Recording: https://ed-ac-uk.zoom.us/rec/share/Qt_qW6IHGW4K0reWxjoAIgNgcs48gQ_siLccucMbHGnOgn9IEXRP2aVq2wSrH_gy.02PSxYcCxnIAJXg1

November 3, 2022

Alexey Korepanov (University of Paris)

Title: Almost sure approximation by Brownian motion for Bunimovich flowersAbstract: I will talk about approximation of processes which appear on Bunimovich flowers (deterministic dynamical systems where a point particle moves inside a table made of several concave arcs, well known for slow memory loss), and about their approximation by a Brownian motion by reconstructing both on the same probability space so that they are close. This is a rather special result about a rather particular system, but in a way it completes a long line of research. I’ll attempt to introduce the topic and explain the kind of problems we are dealing with. This is a joint work in progress with C.Cuny, J.Dedecker and F.Merlevede.

Recording: https://ed-ac-uk.zoom.us/rec/share/KN21bP67RtH98DAUfANo_MtXCtOGvMnri6VbzF8mi3cAUtDydkJwhakSd39QrjJt.x-5UG9mACtygtg4Y

October 27, 2022

Samuel Cohen (University of Oxford)

Title: Neural-SDEs and Market Models of Options

Abstract: Measuring market risk for option portfolios is challenging; it requires modelling joint dynamics of liquid options under the real world measure, simulating realistic trajectories of risk factors, and evaluating option prices efficiently under a large of amount of risk scenarios. In this talk we will construct an arbitrage-free neural-SDE market model for European call options. This involves building neural networks satisfying certain structural assumptions. Through backtesting analysis, we show that our models are more computationally efficient and accurate for evaluating Value-at-Risk (VaR) of option portfolios, with better coverage performance and less procyclicality than standard filtered historical simulation approaches.

Recording: https://ed-ac-uk.zoom.us/rec/share/u7V5IkCcWe8mWoDeWQaDlTP2EW4zDWbz9YBq5PDzmtC9wEJNc2laui6r9vasFh58.xo4YiUvTBeWmKlTI

Karen Habermann (University of Warwick)

Title: A polynomial expansion for Brownian motion and the associated fluctuation process

Abstract: We start by deriving a polynomial expansion for Brownian motion expressed in terms of shifted Legendre polynomials by considering Brownian motion conditioned to have vanishing iterated time integrals of all orders. We further discuss the fluctuations for this expansion and show that they converge in finite dimensional distributions to a collection of independent zero-mean Gaussian random variables whose variances follow a scaled semicircle. We then link the asymptotic convergence rates of approximations for Brownian Lévy area which are based on the Fourier series expansion and the polynomial expansion of the Brownian bridge to these limit fluctuations. We close with a general study of the asymptotic error arising when approximating the Green’s function of a Sturm-Liouville problem through a truncation of its eigenfunction expansion, both for the Green’s function of a regular Sturm-Liouville problem and for the Green’s function associated with the classical orthogonal polynomials.

Comments are closed

Comments to this thread have been closed by the post author or by an administrator.

Toggle navigation menu Menu

Useful Links:

Friday, April 4, 2025

Title: Regularization by multiplicative noise

Abstract:

Tuesday, April 1, 2025

Title: Superdiffusive Central Limit Theorem for the Stochastic Burgers Equation at the critical dimension

Abstract:

Tuesday, March 25, 2025 [Online]

Title: A duality method for mean-field limits with singular interactions

Abstract:

Tuesday, March 18, 2025 [Online]

Title: TASEP and Schubert Kalculus

Abstract:

Wednesday, March 19, 2025

Title: Global dynamics and weak universality for the fractional hyperbolic -model

Abstract:

Tuesday, March 11, 2025 [Online]

Title: Ramanujan Property and Edge Universality of Random Regular Graphs

Abstract:

Tuesday, March 4, 2025

Title: The tree-TASEP on Galton-Watson trees

Abstract:

Tim Johnston (Université Paris Dauphine)

Title: Privacy Guarantees for Stochastic Processes

Abstract:

Tuesday, February 25, 2025 [Online]

Tuesday, February 4, 2025

George Yin (University of Connecticut)

Title: Deep Filtering

Abstract:

Tuesday, January 28, 2025 [Online]

Title: Logarithmically correlated fields from non-Hermitian random matrices

Abstract:

Tuesday, January 21, 2025 [In Person Only]

Title: The incipient infinite cluster in high dimensional percolation: a robust construction

Abstract:

Tuesday, December 3, 2024 [Jointly with Analysis Seminar at UoE]

Title: Self-interacting approximation to McKean-Vlasov long time limit

Abstract:

Title: Refinements of Berry-Esseen inequality in terms of Lyapunov coefficients

Abstract:

Tuesday, November 26, 2024

Title: Airyβ line ensemble

Abstract:

Tuesday, November 19, 2024

Title: Large deviations for the Φ^4_3 measure via Stochastic Quantisation

Abstract:

Roxana Dumitrescu (King’s College London)

Title: A new Mertens decomposition of Y g,ξ-submartingale systems and applications

Abstract:

Verena Schwarz (University of Klagenfurt)

Title: Milstein scheme for McKean–Vlasov SDEs driven by Brownian motion and Poisson random measure

Abstract:

Tuesday, November 12, 2024

Title: Growth of Stationary Hasting-Levitov

Abstract:

Tuesday, November 5, 2024

Title: Some recent progress on the 2DOCP

Abstract:

Title: Nonlinear PDEs with modulated dispersion – regularization by noise

Abstract:

Tuesday, October 15, 2024

Title: Towards Rough Surfaces

Abstract:

Tuesday, October 1, 2024

Joseph Najnudel (University of Bristol)

Title: Circular ensembles, orthogonal polynomials and Gaussian multiplicative chaos

Abstract:

Zahra Sadat Mirsajjadi (University of Edinburgh)

Title: Infinite-dimensional diffusions from random matrix dynamics

Abstract:

Tuesday, September 24, 2024

Title: Reinforcement learning for mean field games and mean field control problems

Abstract:

Thursday, July 4, 2024

Matteo Mucciconi (University of Warwick)

Title: Large Deviations for the height function of the deformed polynuclear growth.

Abstract:

Title: Global dynamics and weak universality for the fractional hyperbolic $\Phi^4_3$ -model

Title: Stochastic quantisation of the fractional $\Phi^4$ model via flow equations