Summary of the Kolmogorov-Obukhov (1941) theory. Part 2: Kolmogorov’s theory in x-space.
Summary of the Kolmogorov-Obukhov (1941) theory. Part 2: Kolmogorov’s theory in x-space.
Kolmogorov worked in $x$-space and his two relevant papers are cited below as [1] (often referred to as K41A) and [2] (K41B). We may make a pointwise summary of this work, along with more recent developments as follows.
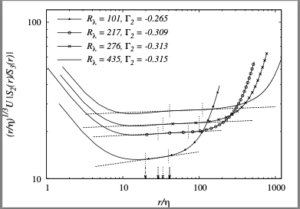
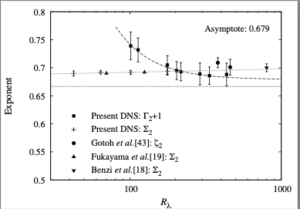
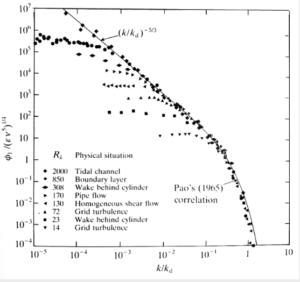
[a] In K41A, Kolmogorov introduced the concepts of local homogeneity and local isotropy, as applying in a restricted range of scales and in a restricted volume of space. He also seems to have introduced what we now call the structure functions, allowing the introduction of scale through the correlations of velocity differences taken between two points separated by a distance $r$. He used Richardson’s concept of a cascade of eddies, in an intuitive way, to introduce the idea of an inertial sub-range, and then used dimensional analysis to deduce that (in modern notation) $S_2 \sim \varepsilon^{2/3}r^{2/3}$.
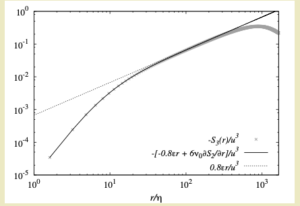
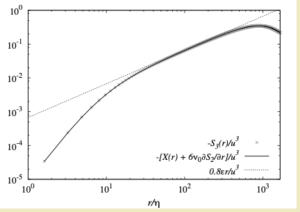
[b] In K41B, he used an ad hoc closure of the Karman-Howarth equation (KHE) to argue that $S_3 = 0.8 \varepsilon r$ in the inertial range of values of $r$: the well-known ‘four-fifths law’. He further assumed that the skewness factor was constant and found that this led to the K41A result for $S_2$. The closure was based on the fact that the term explicit in $S_2$ would vanish as the viscosity tended to zero, whereas its effect could still be retained in the dissipation rate.
[c] In 1947, Batchelor [3] provided an exegesis of both these theories. In the case of K41A, this was only partial, but he did make it clear that K41A relied (at least implicitly) on Richardson’s idea of the ‘eddy cascade’. He also pointed out that K41B could not be readily extended to higher-order equations in the statistical hierarchy, because of the presence of the pressure term with its long-range properties in the higher-order equations.
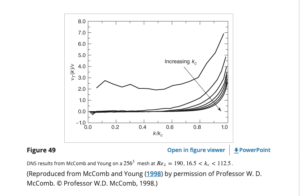
[d] Moffatt [4] credited this paper by Batchelor with bringing Kolmogorov’s work to the Western world. He also, in effect, expressed surprise that Batchelor did not include his re-derivation of K41B in his book. This is a very interesting point; and, in my view, is not unconnected to the fact that Batchelor discussed K41A almost entirely in wavenumber space in his book. I will return to this later.
[e] In 2002, Lundgren re-derived the K41B result, by expanding the dimensionless structure functions in powers of the inverse Reynolds number. By demanding that the expansions matched asymptotically in an overlap region between outer and inner scaling regimes, he was also able to recover the K41A result without the need to make an additional assumption about the constancy of the skewness.
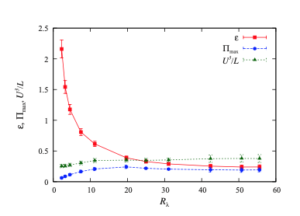
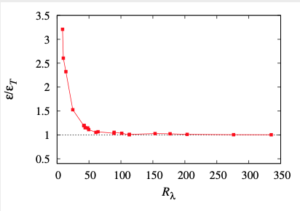
[f] More recently, McComb and Fairhurst [6] used the asymptotic expansion of the dimensionless structure functions to test Kolmogorov’s hypothesis of local stationarity and concluded that it could not be true. They found that the time-derivative must give rise to a constant term; which, however small, violates the K41B derivation of the four-fifths law. Nevertheless, they noted that in wavenumber space, this term (which plays the part of an input to the KHE) will appear as a Dirac delta function at the origin, and hence does not violate the derivation of the minus five-thirds law in $k$-space. We will extend this idea further in the next post.
[1] A. N. Kolmogorov. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. C. R. Acad. Sci. URSS, 30:301, 1941. (K41A)
[2] A. N. Kolmogorov. Dissipation of energy in locally isotropic turbulence. C. R. Acad. Sci. URSS, 32:16, 1941. (K41B)
[3] G. K. Batchelor. Kolmogoroff’s theory of locally isotropic turbulence. Proc. Camb. Philos. Soc., 43:533, 1947.
[4] H. K. Moffatt. G. K. Batchelor and the Homogenization of Turbulence. Annu. Rev. Fluid Mech., 34:19-35, 2002.
[5] Thomas S. Lundgren. Kolmogorov two-thirds law by matched asymptotic expansion. Phys. Fluids, 14:638, 2002.
[6] W. D. McComb and R. B. Fairhurst. The dimensionless dissipation rate and the Kolmogorov (1941) hypothesis of local stationarity in freely decaying isotropic turbulence. J. Math. Phys., 59:073103, 2018.