An assessment of Onsager’s concept of scale invariance: 3

An assessment of Onsager’s concept of scale invariance: 3

I will complete this sequence of posts by discussing the scale-invariance paradox and showing how the Onsager criterion for the inertial range should be modified in order to resolve it.

We begin by noting that the first measurement of the transfer spectrum was made in 1963 by Uberoi, who measured the time-derivative and the viscous dissipation terms in the Lin equation and obtained the transfer spectrum as the remaining term in that equation [1]. He was surprised to find that $T(k,t)$ had a single zero crossing when he had expected that it would be zero over an extended range of wavenumbers, corresponding by simple calculus to an extended region of scale-invariant flux. He attributed this failure to the Reynolds number being too low. However, over the following years it became clear the transfer spectrum only ever has a single zero-crossing at even the highest Reynolds numbers, and so the scale-invariance paradox was born. A fuller account of this topic can be found in the article [2] or the book [3].

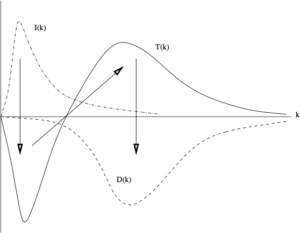
The behaviour of the terms in the Lin equation is illustrated schematically in the figure. Note that the input term is $I(k) =- dE(k,t)/dt$ in this case, whereas if we were considering stationary turbulence it would be the rate of work done by the stirring forces. Further discussion of these points can be found in [3].

It is of interest to note that we can use simple mathematical reasoning to make two general observations from this figure. First, it could have been anticipated that $T(k)$ would only have a single zero-crossing at $k=k_{*}$. Evidently if the input term decreases monotonically as the inertial range is approached from below, while the dissipation spectrum also decreases monotonically as the inertial range is approached from above, then where these two terms are equal at $k=k_{*}$ (say) we must have the single zero of $T(k)$.

Secondly, from equation (9) in the first post in this sequence (on 27 June), we may infer from general conditions of smoothness corresponding to physical behaviour, that the flux must go through a maximum value at $k=k_{*}$. Thus the conclusion of Shanmugasundaram [4] from detailed computations of the LET theory could also have been anticipated.

Let us now consider the Onsager criterion in rather more detail and apply it to the interval $0\leq k \leq k_{*} $. We may write this in terms of the spectral density function $S(k,j)$ as: \begin{equation}\Pi(k_{*})=\int_0^{k_*}T(k)dk=\int_0^{k_*}dk\left[\int_0^\infty dj S(k,j)\right].\end{equation}We may then divide up the range of integration over $j$ at $j=k_{*}$ to obtain:\begin{equation}\Pi(k_{*})=\int_0^{k_{*}}dk=\int_0^{k_{*}}dk\left[\int_0^{k_{*}} dj\,S(k,j)+\int_{k_{*}}^\infty dj\,S(k,j)\right].\end{equation}From the antisymmetry of $S(k,j)$ under the interchange of $k$ and $j$, it follows that the first term in the square brackets gives zero and we are left with: \begin{equation}\Pi(k_{*})=\int_0^{k_{*}}dk\int_{k_{*}}^\infty dj\,S(k,j)\equiv \int_0^{k_{*}}dk T^{-+}(k|k_{*}),\end{equation} where we have introduced the filtered-partitioned form of the spectral transfer function $T^{-+}(k|k_{*})$.

Further details of these filtered-partitioned forms may be found in [2], where some results are cited which suggest that this procedure may resolve the scale-invariance paradox. However our main conclusion here is that it is necessary to introduce such forms, rather than just use $T(k)$, in order to understand results such as [3] and [4], particularly if we are to disentangle the effects of scaling on the Kolmogorov length versus the Taylor microscale.
References
[1] M. S. Uberoi. Energy transfer in isotropic turbulence. Phys. Fluids, 6:1048, 1963.
[2] David McComb. Scale-invariance in three-dimensional turbulence: a paradox and its resolution. J. Phys. A: Math. Theor., 41:75501, 2008.
[3] W. David McComb. Homogeneous, Isotropic Turbulence: Phenomenology, Renormalization and Statistical Closures. Oxford University Press, 2014.
[4] V. Shanmugasundaram. Modal interactions and energy transfers in isotropic turbulence as predicted by local energy transfer theory. Fluid. Dyn. Res, 10:499, 1992.
[5] M. Meldi and J. C. Vassilicos. Analysis of Lundgren’s matched asymptotic expansion approach to the Karman-Howarth equation using the eddy damped quasinormal Markovian turbulence closure. Phys. Rev. Fluids, 6:064602, 2021.