Viscous and forcing corrections to Kolmogorov’s ‘4/5’ law.

The Kolmogorov `4/5′ law for the third-order structure function $S_3(r)$ is widely regarded as the one exact result in turbulence theory. And so it should be: it has a straightforward derivation from the Karman-Howarth equation (KHE), which is an exact energy balance derived from the Navier-Stokes equation. Nevertheless, there is often some confusion around its discussion in the literature. In particular, for stationary isotropic turbulence, there can be confusion about the effects of viscosity (small scales) and forcing (large scales). These aspects have been clarified by McComb et al [1], who used spectral methods to obtain $S_2$ and $S_3$ from a direct numerical simulation of the equations of motion.

If we follow the standard treatment (see [2], Section 4.6.2), we may write: \begin{equation} S_3(r)= -\frac{4}{5}\varepsilon r + 6\nu\frac{\partial S_2}{\partial r}.\end{equation}
In the past, this statement has been criticised because it omits the forcing which must be present in order to sustain a stationary turbulent field. However, it should be borne in mind that this is an entirely local equation; and, if the effect of the forcing is concentrated at the largest scales, then omission of these scales also omits the forcing. We can shed some light on this by reproducing Figure 7 from [1], thus:

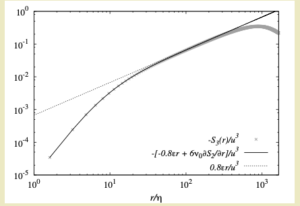
The results were taken at a Taylor-Reynolds number $R_{\lambda} = 435.2$, and show how the departure from the `4/5′ law at the small scales is due to the viscous effects. Clearly there is a range of values of $r$ where the `4/5′ law may be regarded as exact, in the ordinary sense appropriate to experimental work. This range of scales is, of course, the inertial range. Note that $\eta$ is the Kolmororov length scale.

Presumably the departure from the `4/5′ law at the large scales is due to forcing effects, and McComb et al [1] also shed light on this point. They did this by working in spectral space, where stirring forces have been studied since the late 1950s in the context of the statistical theories (e.g Kraichnan, Edwards, Novikov, Herring: see [3] for details) and are correspondingly well understood. They began with the Lin equation: \begin{equation} \frac{\partial E(k,t)}{\partial t} = T(k,t) – 2\nu k^2E(k,t) + W(k), \end{equation} where in principle the energy and transfer spectra depend on time, whereas the spectrum of the stirring forces $W(k)$ is taken as independent of time in order to ensure ultimate stationarity. Thus we will drop the time dependences hereafter as we will only consider the stationary case.

We can derive the KHE from this and the result is the usual KHE plus an input term $I(r)$, defined by: \begin{equation}I(r) = \frac{3}{r^3}\int_0^r\, dy \,y^2\, W(y),\end{equation} where $W(y)$ is the three-dimensional Fourier transform of the work spectrum $W(k)$. By integrating the KHE (as Kolmogorov did in deriving the `4/5′ law) we obtain the form for the third-order structure function $S_3(r)$ as: \begin{equation} S_3(r)=X(r) + 6\nu\frac{\partial S_2}{\partial r},\end{equation}where where $X(r)$ is given in terms of the forcing spectrum by: \begin{equation} X(r) = -12r\int_0^{\infty}\,dk W(k)\,\left[\frac{3\sin kr – 3kr \cos kr-(kr)^2 \sin kr}{(kr)^5}\right].\end{equation}
The result of including the effect of forcing is shown in Figure 8 of [1], which is reproduced here below.

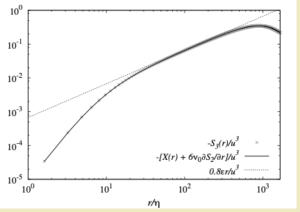
These results are taken from the same simulation as above, and now the contributions from viscous and forcing effects can be seen to account for the departure of $S_3$ from the `4/5′ law at all scales.

In [1] it is pointed out that $X(r)$ is not a correction to K41, as used in other previous studies. Instead, it replaces the erroneous use of the dissipation rate of others’, and contains all the information of the energy input at all scales. In the limit of $\delta(k)$ forcing, $I(y)= \varepsilon_W = \varepsilon$, such that $X(r) = -4\varepsilon\, r/5$, giving K41 in the infinite Reynolds number limit. Note that $\varepsilon_W$ is the rate of doing work by the stirring forces. Further details may be found in [1].

[1] W. D. McComb, S. R. Yoffe, M. F. Linkmann, and A. Berera. Spectral analysis of structure functions and their scaling exponents in forced isotropic turbulence. Phys. Rev. E, 90:053010, 2014.
[2] W. David McComb. Homogeneous, Isotropic Turbulence: Phenomenology, Renormalization and Statistical Closures. Oxford University Press, 2014.
[3] W. D. McComb. The Physics of Fluid Turbulence. Oxford University Press, 1990.

Local isotropy, local homogeneity and local stationarity.

In last week’s post I reiterated the argument that the existence of isotropy implies homogeneity. However, Alex Liberzon commented that there could be inhomogeneous flows that exhibited isotropy on scales that were small compared to the overall size of the flow. This comment has the great merit of drawing attention to the difference between a purely theoretical formulation and one dealing with a real practical situation. In my reply, I mentioned that Kolmogorov had introduced the concept of local isotropy, which supported the view that Alex had put forward. So I thought it would be interesting to look in detail again at what Kolmogorov had actually said. Incidentally, Kolmogorov said it in 1941 but for the convenience of readers I have given the later references, as reprinted in the Proceedings of the Royal Society.

Now, although I like to restrict the problem to purely isotropic turbulence, where it still remains controversial in that many people believe in intermittency corrections or anomalous exponents, Kolmogorov actually put forward a theory of turbulence in general. He argued that a cascade as envisaged by Richardson could lead to a range of scales where the turbulence becomes locally homogeneous. In [1], which I refer to as K41A, he put forward two definitions, which I shall paraphrase rather than quote exactly.

The first of these is as follows: `Definition 1. The turbulence is called locally homogeneous in the domain $G$ if the probability distribution of the velocity differences is independent of the origin of coordinates in space, time and velocity, providing that all such points are contained within the domain $G$.’

We should note that this includes homogeneity in time as well as in space. In other words, Kolmogorov was assuming local stationarity as well.

Then his second definition is: `Definition 2. The turbulence is called locally isotropic in the domain $G$, if it is homogeneous and if, besides, the distribution laws mentioned in Definition 1 are invariant with respect to rotations and reflections of the original system of coordinate axes $(x_1,\,x_2\,x_3)$.’

Note that the emphasis is mine.

Kolmogorov then compared his definition of isotropy to that of Taylor, as introduced in 1935. He stated that his definition is narrower, because he also requires local stationarity, but wider in that it applies to the distribution of the velocity differences, and not to the velocities themselves. Later on, when he derived the so-called ‘$4/5$’ law [2], he had already made the assumption that the time-derivative term could be neglected, and simply quoted the Karman-Howarth equation without it: see equation (3) in [2].

The question then arises, how far do these assumptions apply in any real flow? In my post of 11th February 2021, I conjectured that this might be a matter of the macroscopic symmetry of the flow. For instance, the Kolmogorov picture might apply better in plane channel flow that in plane Couette flow. I plan to return to this point some time.

[1] A. N. Kolmogorov. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. Roy Soc. Lond., 434:9-13, 1991.
[2] A. N. Kolmogorov. Dissipation of energy in locally isotropic turbulence. Proc. Roy Soc. Lond., 434:15-17, 1991.

Is isotropy the same as spherical symmetry?

To which you might be tempted to reply: ‘Who ever thought it was?’ Well, I don’t know for sure, but I’ve developed a suspicion that such a misconception may underpin the belief that it is necessary to specify that turbulence is homogeneous as well as isotropic. When I began my career it was widely understood that specifying isotropy was sufficient, as it was generally realised that homogeneity was a necessary condition for isotropy. A statement to this effect could (and can) be found on page 3 of Batchelor’s famous monograph on the subject [1].

I have posted previously on this topic (my second post, actually, on 12 February 2020) and conceded that the acronym HIT, standing of course for ‘homogeneous, isotropic turbulence’, has its attractions. For a start, it’s the shortest possible way of telling people that you are concerned with isotropic turbulence. I’ve used it myself and will probably continue to do so. So I don’t see anything wrong with using it, as such. The problem arises, I think, when some people think that you must use it. In other words, such people apparently believe that there is an inhomogeneous form of isotropic turbulence.

When you think about it that is really quite worrying. I’m not particularly happy about someone, whose understanding is so limited, refereeing one of my papers. Although, to be honest, that could well explain some of the more bizarre referees’ reports over the years! Anyway, let’s examine the idea that there may be some confusion between isotropy and spherical symmetry.

Isotropy just means that a property is independent of orientation. Spherical symmetry sounds quite similar and is probably the more frequently encountered concept for most of us (at least during our formal education). Essentially it means that, relative to some fixed point, a field only varies with distance from the point but not with angle. A familiar example would be a point electric charge in free space. So we might be tempted to visualise isotropy as a form of spherical symmetry, the common element being the independence of orientation.

The problem with doing this, is that the property of isotropy of a medium must apply to any point within it. Whereas, spherical symmetry depends on the existence of a special point which may be taken as the origin of coordinates. But the existence of such a special point would violate spatial homogeneity. So for isotropy to be true, we must have spatial uniformity or homogeneity. I think that one can infer this mathematically from the fact that the only isotropic tensors are (subject to a scalar multiplier) the Kronecker delta $\delta_{ij}$ and the Levi-Civita density $\epsilon_{ijk}$. So any isotropic tensor must have components that are independent of the coordinates of the system.

For this point applied to the cosmos, i.e. homogeneity is a necessary (but not sufficient) condition for isotropy, see Figure 2 on page 24 of [2]. It seems to be easier to visualise these matters in terms of the night sky which is a fairly (if, illusory) static-looking entity. But when we add in a continuum structure and random variations on many length scales, it can be more difficult. We will come back to this particular problem in my next post.

[1] G. K. Batchelor. The theory of homogeneous turbulence. Cambridge University Press, Cambridge, 2nd edition, 1971.
[2] Steven Weinberg. The first three minutes: a modern view of the origin of the universe. Basic Books, NY, 1993.

Various kinds of turbulent dissipation?

The current interest in Onsager’s conjecture (see my blog of 23 September 2021) has sparked my interest in the nature of turbulent dissipation. Essentially a fluid only moves because a force acts on it and does work to maintain it in motion. The effect of viscosity is to convert this kinetic energy of macroscopic motion into random molecular motion, which is perceived as heat. If there is turbulence, this acts to transfer the macroscopic kinetic energy to progressively smaller scales, where the steeper velocity gradients can dissipate it as heat.

This all seems quite straightforward and well understood. However, Onsager’s conjecture, as a matter of physics, is less easily understood. It interprets the infinite Reynolds number limit as being when the continuum nature of the fluid breaks down. It also implies that, when the Reynolds number becomes very large, the Navier-Stokes equation somehow becomes the Euler equation; which, despite its inviscid nature, satisfactorily accounts for the dissipation. It can do this (supposedly) because it has lost its property of conserving energy. In turn, this is supposed to happen because the velocity is no longer a continuous and differentiable field. Of course there does not seem to be any mechanism for turning the dissipated energy into heat, so the thermodynamic aspects of this process look distinctly dodgy.

There are two other cases where macroscopic kinetic energy is not turned into heat.

The first of these is in large-eddy simulation, which has for many years been widely studied for its practical significance. This of course is not a physical situation. It is purely a method of simulating turbulence numerically without being able to resolve all the scales: an introduction can be found in [1]. The central problem is to model the flow of energy to the scales which are too small to be resolved: the so-called subgrid drain. Various models have been studied for the subgrid viscosity, while a novel approach is the operational method of Young and McComb [2]. In this latter, an algorithm is used to feed back energy into the resolved modes, such that the spectral shape is kept constant. In fact this method can be interpreted in terms of an effective subgrid viscosity which is very similar to that found in conventional simulations when a large-eddy simulation is compared to a fully resolved one. But, so far as I know, no one has considered modelling the temperature rise that would be due to the viscous dissipation in these cases.

The second case is the direct simulation of the Euler equation. Such simulations can only lead to thermal equilibrium but naturally the simulations must be truncated to a finite number of modes, to avoid having an infinite amount of energy. However, in 2005, some interesting transient behaviour was been found in truncated Euler simulations [3] and confirmed the following year by the use of a closure approximation [4]. These simulations may be divided in terms of their energy spectra into two spectral ranges: a Kolmogorov range and an equipartition range. A buffer range in between these two is described by Bos and Bertoglio as a ‘quasi-dissipative’ zone, which is another example of non-viscous dissipation. However, it can only exist for a finite time and ultimately the system must move to thermal equilibrium.

I think it would be interesting to see one of the proponents of Onsager’s conjecture explain the simple physics of how the conjectured situation came about with increasing Reynolds number. All the mathematical expressions you need to do that are available. But I don’t think I will see that any time soon!

[1] W. D. McComb. The Physics of Fluid Turbulence. Oxford University Press, 1990.
[2] A. J. Young and W. D. McComb. Effective viscosity due to local turbulence interactions near the cutoff wavenumber in a constrained numerical simulation. J. Phys. A, 33:133-139, 2000.
[3] Cyril Cichowlas, Pauline Bonatti, Fabrice Debbasch, and Marc Brachet. Effective Dissipation and Turbulence in Spectrally Truncated Euler Flows. Phys. Rev. Lett., 95:264502, 2005.
[4] W. J. T. Bos and J.-P. Bertoglio. Dynamics of spectrally truncated inviscid turbulence. Phys. Fluids, 18:071701, 2006.