Turbulent dissipation and the two cultures?

Turbulent dissipation and the two cultures?
I recently saw the paper cited as [1] below, which for me is I think the first of the 2021 papers. As the title suggests, it presents a review of methods of measuring the turbulent dissipation rate. It contains a certain amount of basic theory, along the lines of expressions for the dissipation rate, the Taylor dissipation surrogate, remarks about the role of inertial transfer, dynamical equilibrium, and so on. But there is no attempt at a statistical theory and most theoretical attempts at explaining the dependence of the dissipation rate $\varepsilon$ on the Taylor-Reynolds number do not get a mention.

Nevertheless, the authors do cite a paper by my co-authors and me, which presents an analytical theory of the dependence of the normalized dissipation $C_{\varepsilon}$, which is the dissipation rate divided by $U^3/L$, where $U$ is the root mean square velocity and $L$ is the integral lengthscale [2]. They say that we `explained that the decay of the dimensionless dissipation with increasing Reynolds number was because of the increase in the Taylor surrogate’. This is true for forced, stationary turbulence, because we can keep the rate of forcing (and hence the dissipation) constant while decreasing the viscosity in order to increase the Reynolds number.

However, this paper says so much more! It presents an analytical theory, based on the Karman-Howarth equation, in which dimensionless structure functions are expanded in inverse powers of the Reynolds number. The resulting expression is given by: \begin{equation}C_{\varepsilon}= C_{\varepsilon,\infty}+C/R_L + O(1/R^2_L), \end{equation} where $R_L$ is the integral scale Reynolds number. Direct numerical simulation was used to obtain the coefficients as $C=18.9 \pm 0.009$ and $C_{\varepsilon,\infty}= 0.468\pm0.006$. The result compared to other numerical investigations is shown in the figure below, which is taken from Fig. 1 of [2], and where equation (44) of that reference is the equation just given here.

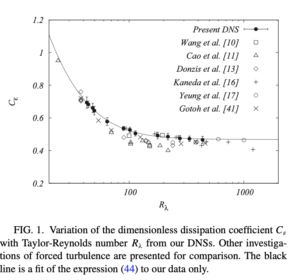
It is worth emphasising that this result is asymptotically exact in the limit of large Reynolds numbers. For low Reynolds numbers, our DNS confirmed that the $1/R_L$ dependence was correct to within experimental error. When this theory was later applied to magnetohydrodynamic turbulence, it was found necessary to include a term at order $1/R^2_L$ at low Reynolds numbers [3]. In fact, a detailed argument was previously put forward by us to the effect that the $1/R_L$ dependence was exact for isotropic turbulence: see the supplemental material to the paper cited as [4] below.

I should also emphasise that none of this is intended as a criticism of Wang et al, which is a perfectly competent piece of work of its general type. It is really a matter of emphasising the gulf between fluid dynamics and physics. For instance, it would be very unlikely that an experimental particle physicist would fail to see the point of a paper by a theoretical particle physicist, even if they were unable to follow the detailed derivations in it. This is because in physics we all have the same education up to a certain level, and even thereafter there is overlap and much in common. But fluid dynamics is much less homogeneous than physics and this leads to misunderstandings based very largely on cultural gaps. Those of us who belong to the very small number of physicists working on turbulence have much cause to be aware of this. I have posted about this before and I will do so soon again!

[1] Guichao Wang et al. Estimation of the dissipation rate of turbulent kinetic energy: A review. Chem. Eng. Science, 229:11633, 2021.
[2] W. D. McComb, A. Berera, S. R. Yoffe, and M. F. Linkmann. Energy transfer and dissipation in forced isotropic turbulence. Phys. Rev. E, 91:043013, 2015.
[3] M. F. Linkmann, A. Berera, W. D. McComb, and M. E. McKay. Nonuniversality and Finite Dissipation in Decaying Magnetohydrodynamic Turbulence. Phys. Rev. Lett., 114:235001, 2015.
[4] W. David McComb, Arjun Berera, Matthew Salewski, and Sam R. Yoffe. Taylor’s (1935) dissipation surrogate reinterpreted. Phys. Fluids, 22:61704, 2010.